 Using the Definition to Compute the Derivative - Exercise 3
Using the Definition to Compute the Derivative - Exercise 3
Exercise 3. We say that the graph of f(x) has a cusp at (a,f(a)), if f(x) is continuous at a and if the
following two conditions hold:
- 1.
-
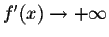 as
as
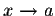 from one side (left or right);
from one side (left or right);
- 2.
-
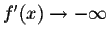 as
as
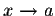 from the other side.
from the other side.
Determine whether
f(x) = x4/3 and
g(x) = x3/5 have a
cusp at (0,0).
Answer. For 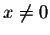 ,
we have
,
we have
So
f(x) does not have a cusp at 0. In fact, the graph has a
horizontal tangent line at (0,0).
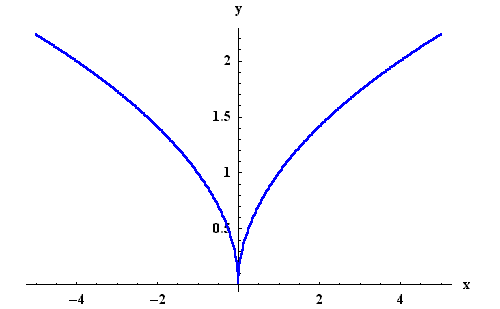
For the function g(x), we have
In this case, we have
So again (0,0) is not a cusp for g(x). But in this case, the
graph has a vertical tangent at this point. Remember that a
vertical line does not have a slope. So the derivative of g(x)at 0 does not exist.
[Back]
[Next]
[Trigonometry]
[Calculus]
[Geometry]
[Algebra]
[Differential Equations]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi
Helmut Knaust
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Using the Definition to Compute the Derivative - Exercise 3
Using the Definition to Compute the Derivative - Exercise 3
 Using the Definition to Compute the Derivative - Exercise 3
Using the Definition to Compute the Derivative - Exercise 3
![]() ,
we have
,
we have
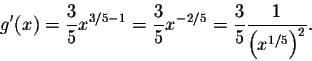
 S.O.S MATHematics home page
S.O.S MATHematics home page