Techniques of Differentiation

Maybe the easiest and most useful formulas are the ones that say that the derivative is linear:

$$\begin{array}{ll} (f + g)'(a) = f'(a) + g'(a)\\ (cf)'(a) = c f'(a)\\ \end{array}$$

Combined with the formula (xⁿ)' = n x^n-1, we see that every polynomial function has a derivative at any point.

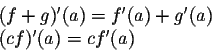
Example. For P(x) = 1-2x + 3x⁴ -5 x⁶, we have

$$P'(x) = -2 + 12 x^3 - 30 x^5\cdot$$

The next two formulas are the most powerful ones. They deal with the derivative of a product and a quotient. They are commonly called the product rule and the quotient rule. We have

$$\begin{array}{lcl} \Big(f\;g\Big)'(a) &=& f'(a)g(a) + f(a) g'... ...splaystyle \frac{f'(a)g(a) - f(a) g'(a)}{g^2(a)}\\ \end{array}$$

In particular, we have

$$\left(\frac{1}{f}\right)'(a) = - \frac{f'(a)}{f^2(a)}\cdot$$

So, we have

$$\left(\frac{1}{x^n}\right)' = - \frac{nx^{n-1}}{x^{2n}} = -n x^{-n-1}$$

which means that the formula (x^r)' = r x^r-1 is also valid for negative exponents.

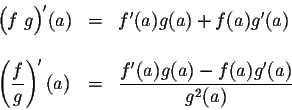
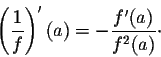
Before we discuss the derivative of trigonometric functions, let us stop here and reflect a little bit more on polynomial functions. Indeed, we saw that the derivative of a polynomial function is also a polynomial function. So we can take another derivative and generate a new function. This function is called the second derivative. We can keep doing this as long as we want to. The functions obtained are called higher derivatives. The common notations used for them are

$$\begin{array}{llllllll} f'(x), &\; f''(x), &\; f'''(x), &\; f... ... &\; \cdots, &\;\displaystyle \frac{d^ny}{dx^n} \\ \end{array}$$

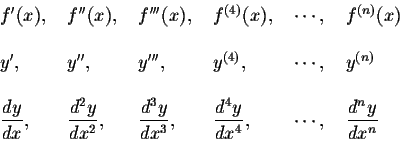
Exercise 1. Find the derivative of the function

$$f(x) = \frac{ax+b}{cx+d}\cdot$$

Is there a nice way to rewrite this derivative?

Answer.

Exercise 2. Find the derivative of

$$f(x) = \frac{\sqrt{x}}{x^2 - x + 3}$$

Answer.

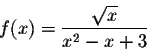
Exercise 3. Solve the equation 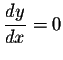$$\frac{dy}{dx} = 0$$ when

$$y = \frac{x^2 - x + 5}{2x+3}$$

Answer.

Exercise 4. Find the points on the graph of y = x^3/2 - x^1/2 at which the tangent line is parallel to the line y+2x = 1. Also find the points on the same graph at which the tangent line is perpendicular to the line y-x = 3.

Answer.

[Back] [Next] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour