 Using the Definition to Compute the Derivative
Using the Definition to Compute the Derivative
 Using the Definition to Compute the Derivative
Using the Definition to Compute the Derivative
We have seen in the previous page how the derivative is defined:
For a function f(x), its derivative at x=a is defined by
Example 1. Let us start with the function
f(x) = x2. We
have
What about the derivative of
f(x) = xn. Similar calculations,
using the binomial expansion for (x+y)n (Pascal's Triangle),
yield
Example 2. Consider the function f(x)=1/x for ![]() .
We have
.
We have
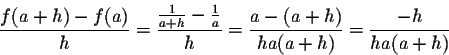
Consequently,
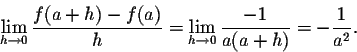
Have you noticed? The algebraic trick in both of the examples above has been to factor out "h" in the numerator, so that we can cancel it with the "h" in the denominator! This is what you try to do whenever you are asked to compute a derivative using the limit definition.
You may believe that every function has a derivative. Unfortunately that is not the case.
Example 3. Let us discuss the derivative of
f(x) = |x| at
0. We have
Remark. This example is interesting. Even though the derivative at the point does not exist, the right and the left limit of the ratio do exist. In fact, if we use the slope-interpretation of the derivative we see that this means that the graph has two lines close to it at the point under consideration. They could be seen as "half-tangents". See Picture.
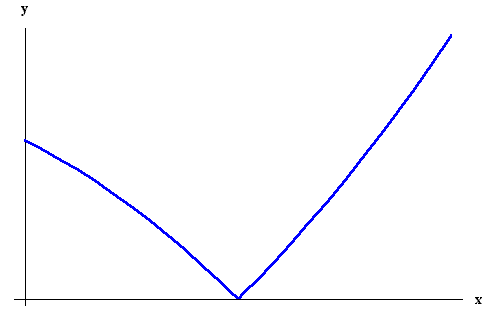 |
So let's push it a little bit more and ask whether a function always has a tangent or half-tangents at any point. That is not the case either.
Example 4. Let us consider the function
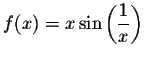 for
for ![]() ,
with
f(0) = 0. We have
,
with
f(0) = 0. We have
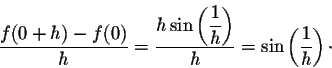
 has no limit when x goes to 0. So the
function has no derivative and no half-derivatives as well at x=0.
has no limit when x goes to 0. So the
function has no derivative and no half-derivatives as well at x=0.
What else can go wrong?
Example 5. Consider the function
![]() .
Then
we have
.
Then
we have
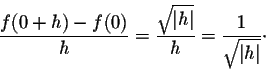
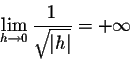
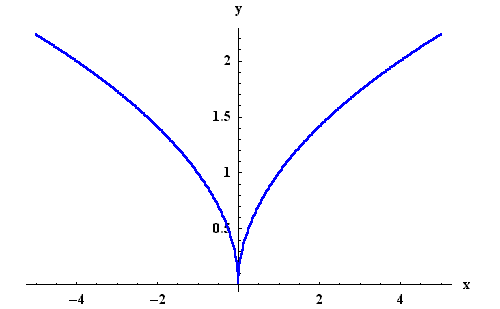 |
In fact, the way the concept of the tangent line was introduced
is based on the notion of slope. You already know that vertical
lines do not have slopes. So we say that the derivative does not
exist whenever the tangent line is vertical. Nevertheless keep in
mind that when the limit giving the derivative is
![]() then the function has a vertical tangent line at the point.
then the function has a vertical tangent line at the point.
It can be quite laborious (or impossible) to compute the derivative by hand as we have done so far. In the next pages we will show how techniques of differentiation help bypass the limit calculations and make our life much easier.
Exercise 1. Find the derivative of
Exercise 2. Discuss the differentiability of
Exercise 3. We say that the graph of f(x) has a cusp at (a,f(a)), if f(x) is continuous at a and if the following two conditions hold:
 |
Determine whether f(x) = x4/3 and g(x) = x3/5 have a cusp at (0,0).
Exercise 4. Show that if f '(a) exists, then we have
Exercise 5. A spherical balloon is being inflated. Find the rate at which its volume V is changing with respect to the radius.
 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi