 The Pinching or Sandwich Theorem
The Pinching or Sandwich Theorem
 The Pinching or Sandwich Theorem
The Pinching or Sandwich Theorem
As a motivation let us consider the function
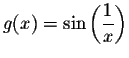 fails to have a limit. So we
are not able to use the basic properties discussed in the previous
pages. But we know that this function
fails to have a limit. So we
are not able to use the basic properties discussed in the previous
pages. But we know that this function
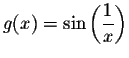 is bounded below by -1 and
above by 1, i.e.
is bounded below by -1 and
above by 1, i.e.
This is an example for the following general result:
Theorem: The "Pinching" or "Sandwich" Theorem Assume that
Example. Let f(x) be a function such that
![]() ,
for any
,
for any ![]() .
The Sandwich Theorem implies
.
The Sandwich Theorem implies
Exercise 2. Use the Sandwich Theorem to prove that
Exercise 3. Consider the function
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
![]()
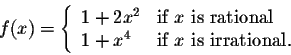
Use the Sandwich Theorem to prove that
![]()
 S.O.S MATHematics home page
S.O.S MATHematics home page
Helmut Knaust
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour