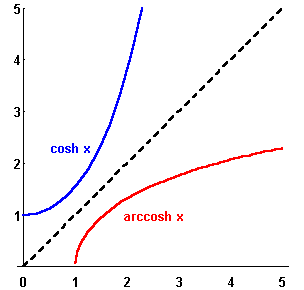
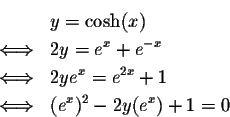Since 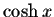 is defined in terms of the exponential function, you should not be surprised that its inverse function can be expressed in terms of the logarithmic function:
is defined in terms of the exponential function, you should not be surprised that its inverse function can be expressed in terms of the logarithmic function:
Let's set
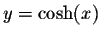 ,
keep in mind that we restrict to
,
keep in mind that we restrict to 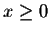 ,
and try to solve for x:
,
and try to solve for x:
This is a quadratic equation
with ex instead of x as the variable. y will be considered a constant.
So using the quadratic formula, we obtain
Since 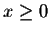 we have that
we have that 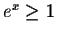 for all x, and since
for all x, and since
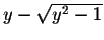 fails to exceed 1 for some y, we have to discard the solution with the minus sign, so
fails to exceed 1 for some y, we have to discard the solution with the minus sign, so
and consequently
Read that last sentence again slowly!
We have found out that
Helmut Knaust
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour

![]() is defined in terms of the exponential function, you should not be surprised that its inverse function can be expressed in terms of the logarithmic function:
is defined in terms of the exponential function, you should not be surprised that its inverse function can be expressed in terms of the logarithmic function:
![]() ,
keep in mind that we restrict to
,
keep in mind that we restrict to ![]() ,
and try to solve for x:
,
and try to solve for x: