The Addition Formulas The Addition Formulas
The fundamental identities are very important for the analysis of trigonometric expressions and functions but they are a direct result of the intimate relation between trigonometry and geometry. The power behind the algebraic nature of trigonometry is hidden and can be measured only with the addition formulas
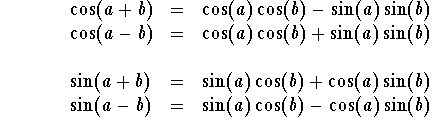
and
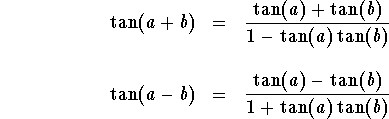
Of course, we used the fact that
Example. verify the identity
Answer. We have
which gives
But
and since
and 
, we get finally
Remark. In general it is good to check whether the given formula is correct. One way to do that is to substitute some numbers for the variables. For example, if we take a=b = 0, we get
or we may take 
. In this case we have
Example. Find the exact value of
Answer. We have
Hence, using the additions formulas for the cosine function we get
Since
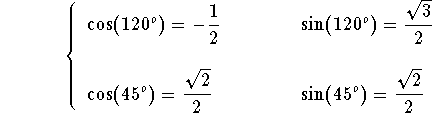
we get
Example. Find the exact value for
Answer. We have
Since
we get
Finally we have
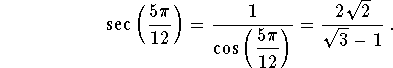
Remark. Using the addition formulas, we generate the following identities
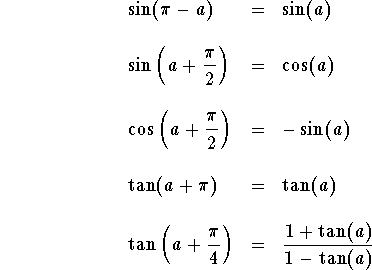
More identities may be proved similar to the above ones. The bottom line is to remember the addition formulas and use them whenever needed.
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi