EXERCISE 3 EXERCISE 3
Assume that City A and City B are located on the same
meridian in the Northern hemisphere and that the earth is a sphere of
radius 4000 mi.
The latitudes of City A and City B are
and 
, respectively.
Solution: For parts (a) and (b), proceed as in Exercise 2:
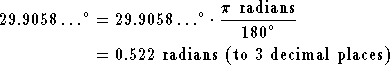
Similarly, 
(c)
We use the Equation 
, where s is the distance along the
surface of the earth between the two cities, R is the radius of the
earth, and 
is the central angle between the two cities, that
is, the difference in their latitudes. The distance between the two
cities is then:
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Luis Valdez Sanchez