 The Derivative
The Derivative The Derivative
The Derivative

The derivative of the function f(x) at the point ![]() is given and
denoted by
is given and
denoted by
![]()
In the table below, u,v, and w are functions of the variable
x. a, b, c, and n are constants (with some restrictions
whenever they apply). ![]() designate the natural logarithmic
function and e the natural base for
designate the natural logarithmic
function and e the natural base for ![]() . Recall that
. Recall that ![]() .
.
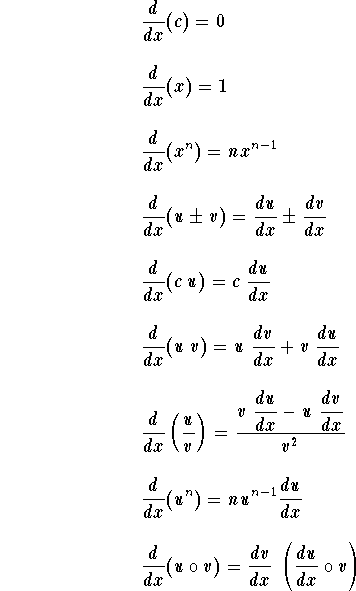
Chain Rule
The last formula
![]()
is known as the Chain Rule formula. It may be rewritten as
![]()
Another similar formula is given by

The inverse of the function y(x) is the function x(y), we have

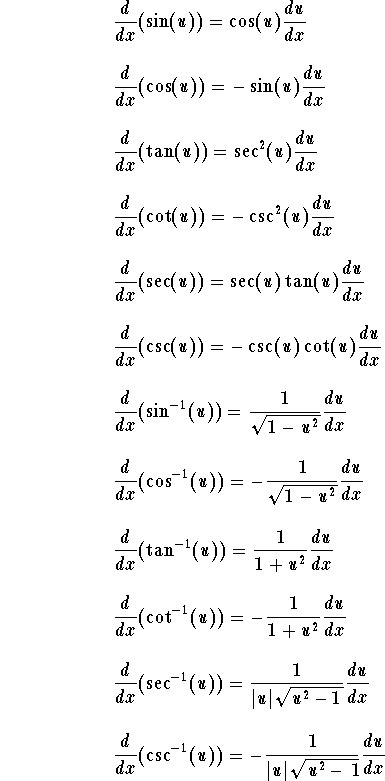
Recall the definitions of the trigonometric functions
![]()
![]()

Recall the definition of the logarithm function with base a > 0
(with ![]() ):
):
![]()
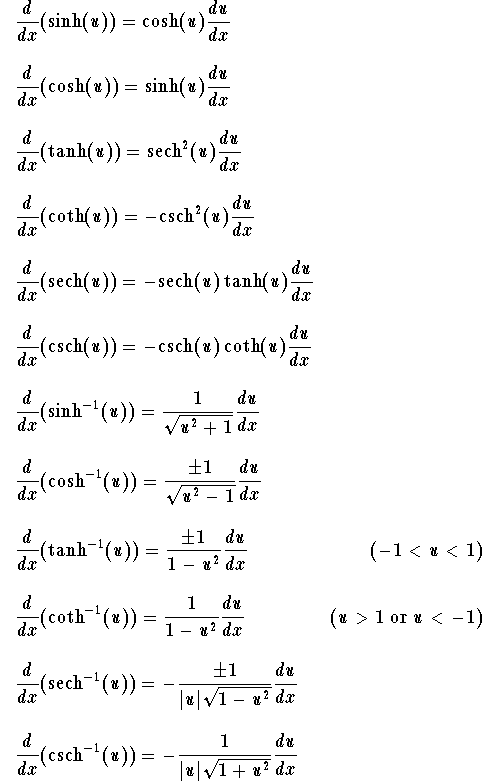
Recall the definitions of the trigonometric functions
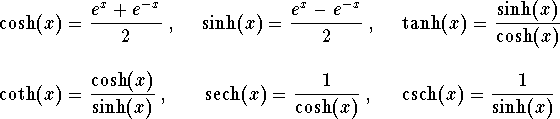
Let y = f(x). We have:

In some books, the following notation for higher derivatives is also used:
![]()
![]()
where ![]() are
the binomial coefficients. For example, we have
are
the binomial coefficients. For example, we have
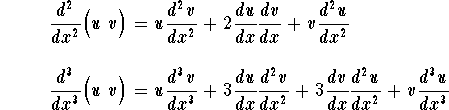

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
