Bernoulli and Euler's Numbers

Definition. The Bernoulli numbers are defined by

$$\begin{array}{lclrl} \displaystyle \frac{x}{e^x - x} &=& 1 - ... ...B_3x^6}{6!}+ \cdots &\mbox{$\vert x\vert < \pi$}\\ \end{array}$$

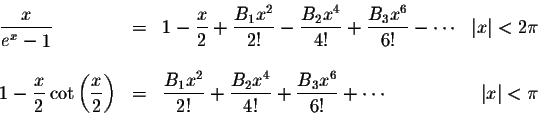
Definition. The Euler numbers are defined by

$$\begin{array}{lccclrl} \mbox{sech}(x) &=& \displaystyle \frac... ...E_3x^6}{6!}+ \cdots &\mbox{$\vert x\vert < \pi$}\\ \end{array}$$

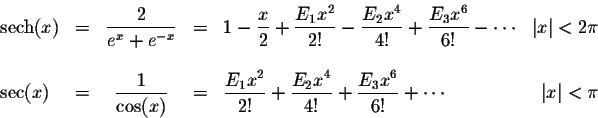
Some Important Formulas.

1.

$B_n = \displaystyle \frac{(2n)!}{2^{2n-1}\pi^{2n}} \left(1 + \displaystyle \frac{1}{2^{2n}} + \displaystyle \frac{1}{3^{2n}} + \cdots \right)$

2.

$B_n = \displaystyle \frac{2(2n)!}{(2^{2n-1}-1)\pi^{2n}} \left(1 - \displaystyle \frac{1}{2^{2n}} + \displaystyle \frac{1}{3^{2n}} - \cdots \right)$

3.

$E_n = \displaystyle \frac{2^{2n+2}(2n)!}{\pi^{2n+1}} \left(1 - \displaystyle \frac{1}{3^{2n+1}} + \displaystyle \frac{1}{5^{2n+1}} - \cdots \right)$

4.

For large n, we have

$$B_n \sim 4 n^{2n} (\pi e)^{-2n} \sqrt{n\pi} = 4 \left(\displaystyle \frac{n}{\pi e}\right)^{2n} \sqrt{n \pi}$$

Below you may find some values of the Bernoulli numbers:

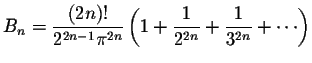
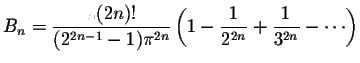
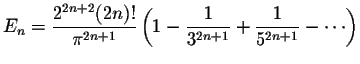
and Euler numbers

[Tables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2023 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour