SYSTEMS OF EQUATIONS
SYSTEMS OF EQUATIONS
A system of equations is a collection of two or more equations with a same set of unknowns. In solving a system of equations, we try to find values for each of the unknowns that will satisfy every equation in the system.
The equations in the system can be linear or non-linear. This tutorial
reviews systems of linear equations.
The problem can be expressed in narrative form or the problem can be
expressed in algebraic form.
Example of a narrative statement of a system of the equations:
The air-mail rate for letters to Europe is 45 cents per half-ounce and to
Africa as 65 cents per half-ounce. If Shirley paid $18.55 to send 35 half-ounce
letters abroad, how many did she send to Africa?
Example of an algebraic statement of the same system of the
equations:
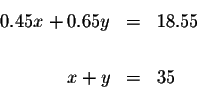
A system of linear equations can be solved four different ways:
Substitution
Gaussian Elimination
Matrices
Graphing
In this review, we are going to show you how to convert a narrative
statement of the problem to an equivalent algebraic of the problem. In other
words, we are going to show you how to translate word problems in to
algebraic equations.
We are also going to show you how to work and check each example by each of
the four methods. The review has several levels. If you find that you easily
understand the example, you can go on to new material. If you are having
trouble with an example, you can work many examples of the same type and
difficulty. We have imbedded the tutorial with many self-tests. At any time
during your review, you may test your knowledge of the material
covered.
This tutorial will cover systems in two variables, three variables, and four variables.
Click on the system you wish to review:
Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author: Nancy Marcus
