Determinant and Inverse of Matrices

Finding the inverse of a matrix is very important in many areas of science. For example, decrypting a coded message uses the inverse of a matrix. Determinant may be used to answer this problem. Indeed, let A be a square matrix. We know that A is invertible if and only if $\det(A) \neq 0$ . Also if A has order n, then the cofactor A_i,j is defined as the determinant of the square matrix of order (n-1) obtained from A by removing the row number i and the column number j multiplied by (-1)^i+j. Recall

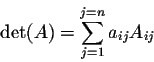
$\begin{displaymath}\det(A) = \sum_{j=1}^{j=n} a_{ij} A_{ij}\end{displaymath}$

for any fixed i, and

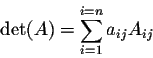
$\begin{displaymath}\det(A) = \sum_{i=1}^{i=n} a_{ij} A_{ij}\end{displaymath}$

for any fixed j. Define the adjoint of A, denoted adj(A), to be the transpose of the matrix whose ij^th entry is A_ij.

Example. Let

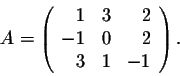
$\begin{displaymath}A = \left(\begin{array}{rrr} 1&3&2\\ -1&0&2\\ 3&1&-1\\ \end{array}\right).\end{displaymath}$

We have

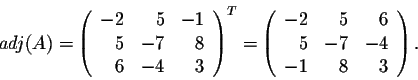
$\begin{displaymath}adj(A) = \left(\begin{array}{rrr} -2&5&-1\\ 5&-7&8\\ 6&-4&3... ...{array}{rrr} -2&5&6\\ 5&-7&-4\\ -1&8&3\\ \end{array}\right).\end{displaymath}$

Let us evaluate $A \cdot adj(A)$ . We have

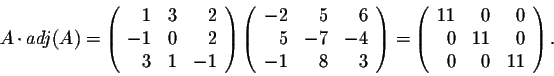
$\begin{displaymath}A \cdot adj(A) = \left(\begin{array}{rrr} 1&3&2\\ -1&0&2\\ ... ...n{array}{rrr} 11&0&0\\ 0&11&0\\ 0&0&11\\ \end{array}\right).\end{displaymath}$

Note that $\det(A) = 11$ . Therefore, we have

$\begin{displaymath}A \cdot adj(A) = \det(A) I_3.\end{displaymath}$

Is this formula only true for this matrix, or does a similar formula exist for any square matrix? In fact, we do have a similar formula.

Theorem. For any square matrix A of order n, we have

$\begin{displaymath}A \cdot adj(A) = \det(A) I_n.\end{displaymath}$

In particular, if $\det(A) \neq 0$ , then

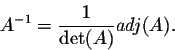
$\begin{displaymath}A^{-1} = \frac{1}{\det(A)} adj(A).\end{displaymath}$

For a square matrix of order 2, we have

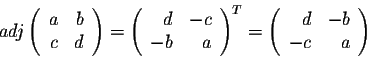
$\begin{displaymath}adj \left(\begin{array}{rr} a&b\\ c&d\\ \end{array}\right) ... ...^T = \left(\begin{array}{rr} d&-b\\ -c&a\\ \end{array}\right)\end{displaymath}$

which gives

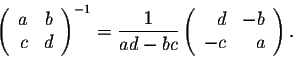
$\begin{displaymath}\left(\begin{array}{rr} a&b\\ c&d\\ \end{array}\right)^{-1}... ...bc} \left(\begin{array}{rr} d&-b\\ -c&a\\ \end{array}\right).\end{displaymath}$

This is a formula which we used on a previous page.

On the next page, we will discuss the application of the above formulas to linear systems.

[Geometry] [Algebra] [Trigonometry ] [Calculus] [Differential Equations] [Matrix Algebra]
S.O.S MATH: Home Page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: M.A. Khamsi

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour