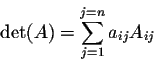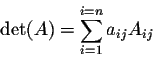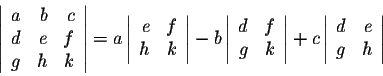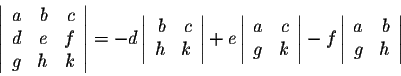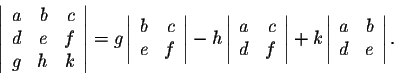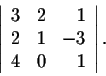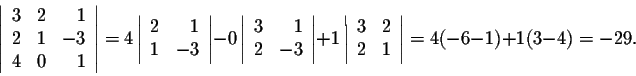Determinants of Matrices of Higher Order
Determinants of Matrices of Higher Order

As we said before, the idea is to assume that previous properties satisfied by the determinant of matrices of order 2, are still valid in general. In other words, we assume:
- 1.
- Any matrix A and its transpose have the same determinant, meaning
- 2.
- The determinant of a triangular matrix is the product of the entries on the diagonal.
- 3.
- If we interchange two rows, the determinant of the new matrix is the opposite of the old one.
- 4.
- If we multiply one row with a constant, the determinant of the new matrix is the determinant of the old one multiplied by the constant.
- 5.
- If we add one row to another one multiplied by a constant, the determinant of the new matrix is the same as the old one.
- 6.
- We have
In particular, if A is invertible (which happens if and only if
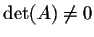 ), then
), then
So let us see how this works in case of a matrix of order 4.
Example. Evaluate
We have
If we subtract every row multiplied by the appropriate number from the first row, we get
We do not touch the first row and work with the other rows. We interchange the second with the third to get
If we subtract every row multiplied by the appropriate number from the second row, we get
Using previous properties, we have
If we multiply the third row by 13 and add it to the fourth, we get
which is equal to 3. Putting all the numbers together, we get
These calculations seem to be rather lengthy. We will see later on that a general formula for the determinant does exist.
Example. Evaluate
In this example, we will not give the details of the elementary operations. We have
Example. Evaluate
We have
General Formula for the Determinant
Let A be a square matrix of order n. Write
A = (aij), where aij is the entry on the row number i and the column number j, for
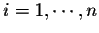 and
and
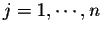 .
For any i and j, set Aij (called the cofactors) to be the determinant of the square matrix of order (n-1) obtained from A by removing the row number i and the column number j multiplied by
(-1)i+j. We have
.
For any i and j, set Aij (called the cofactors) to be the determinant of the square matrix of order (n-1) obtained from A by removing the row number i and the column number j multiplied by
(-1)i+j. We have
for any fixed i, and
for any fixed j. In other words, we have two type of formulas: along a row (number i) or along a column (number j). Any row or any column will do. The trick is to use a row or a column which has a lot of zeros.
In particular, we have along the rows
or
or
As an exercise write the formulas along the columns.
Example. Evaluate
We will use the general formula along the third row. We have
Which technique to evaluate a determinant is easier ? The answer depends on the person who is evaluating the determinant. Some like the elementary row operations and some like the general formula. All that matters is to get the correct answer.
Note that all of the above properties are still valid in the general case. Also you should remember that the concept of a determinant only exists for square matrices.

[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Differential Equations]
[Matrix Algebra]
 S.O.S MATH: Home Page
S.O.S MATH: Home Page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: M.A. Khamsi
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Determinants of Matrices of Higher Order
Determinants of Matrices of Higher Order Determinants of Matrices of Higher Order
Determinants of Matrices of Higher Order
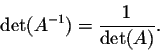

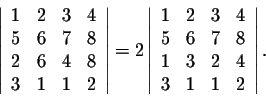
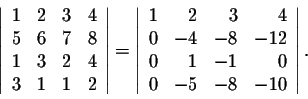
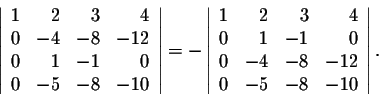
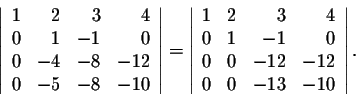
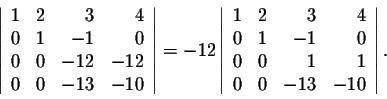
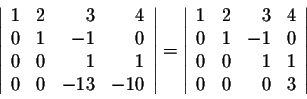
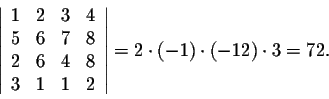
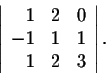
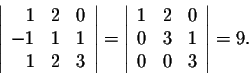
![]() and
and
![]() .
For any i and j, set Aij (called the cofactors) to be the determinant of the square matrix of order (n-1) obtained from A by removing the row number i and the column number j multiplied by
(-1)i+j. We have
.
For any i and j, set Aij (called the cofactors) to be the determinant of the square matrix of order (n-1) obtained from A by removing the row number i and the column number j multiplied by
(-1)i+j. We have