 Complex numbers as Matrices
Complex numbers as Matrices

In this section, we use matrices to give a representation of complex numbers. Indeed, consider the set
We will write
Clearly, the set 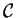 is not empty. For example, we have
is not empty. For example, we have
In particular, we have
for any real numbers a, b, c, and d.
Algebraic Properties of 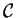
- 1.
- Addition: For any real numbers a, b, c, and d, we have
Ma,b + Mc,d = Ma+c,b+d.
In other words, if we add two elements of the set 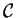 ,
we still get a matrix in
,
we still get a matrix in 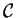 .
In particular, we have
.
In particular, we have
-Ma,b = M-a,-b.
- 2.
- Multiplication by a number: We have
So a multiplication of an element of 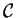 and a number gives a matrix in
and a number gives a matrix in 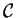 .
.
- 2.
- Multiplication: For any real numbers a, b, c, and d, we have
In other words, we have
Ma,b Mc,d = Mac-bd, ad+bc.
This is an extraordinary formula. It is quite conceivable given the difficult form of the matrix multiplication that, a priori, the product of two elements of 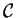 may not be in
may not be in 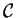 again. But, in this case, it turns out to be true.
again. But, in this case, it turns out to be true.
The above properties infer to 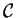 a very nice structure. The next natural question to ask, in this case, is whether a nonzero element of
a very nice structure. The next natural question to ask, in this case, is whether a nonzero element of 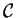 is invertible. Indeed, for any real numbers a and b, we have
is invertible. Indeed, for any real numbers a and b, we have
So, if
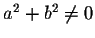 ,
the matrix Ma,b is invertible and
,
the matrix Ma,b is invertible and
In other words, any nonzero element Ma,b of 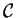 is invertible and its inverse is still in
is invertible and its inverse is still in 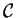 since
since
In order to define the division in 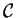 ,
we will use the inverse. Indeed, recall that
,
we will use the inverse. Indeed, recall that
So for the set 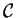 ,
we have
,
we have
Ma, b÷
Mc, d =
Ma, b×
Mc, d-1 =
Ma, b×
M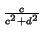 ,
,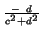
which implies
Ma, b÷
Mc, d =
M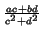 , -
, - 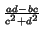
The matrix Ma,-b is called the conjugate of Ma,b. Note that the conjugate of the conjugate of Ma,b is Ma,b itself.
Fundamental Equation. For any Ma,b in 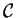 ,
we have
,
we have
Ma,b = a M1,0 + b M0,1 = a I2 + b M0,1.
Note that
M0,1 M0,1 = M-1,0 = - I2.
Remark. If we introduce an imaginary number i such that i2 = -1, then the matrix Ma,b may be rewritten by
a + bi
A lot can be said about 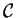 ,
but we will advise you to visit the page on complex numbers.
,
but we will advise you to visit the page on complex numbers.

[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Differential Equations]
[Matrix Algebra]
 S.O.S MATH: Home Page
S.O.S MATH: Home Page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: M.A. Khamsi
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Complex numbers as Matrices
Complex numbers as Matrices Complex numbers as Matrices
Complex numbers as Matrices
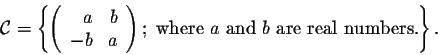
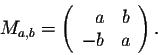
![]()
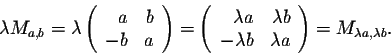
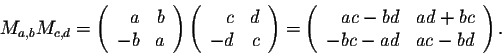
![]() a very nice structure. The next natural question to ask, in this case, is whether a nonzero element of
a very nice structure. The next natural question to ask, in this case, is whether a nonzero element of ![]() is invertible. Indeed, for any real numbers a and b, we have
is invertible. Indeed, for any real numbers a and b, we have
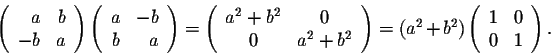
![]() ,
the matrix Ma,b is invertible and
,
the matrix Ma,b is invertible and
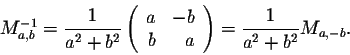
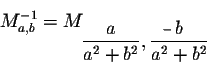
![]() ,
we will use the inverse. Indeed, recall that
,
we will use the inverse. Indeed, recall that
![]() ,
we have
,
we have
![]() ,
but we will advise you to visit the page on complex numbers.
,
but we will advise you to visit the page on complex numbers.

