 Vector Representations of Solutions
Vector Representations of Solutions Vector Representations of Solutions
Vector Representations of Solutions

Consider the linear system of differential equations
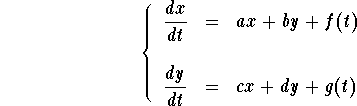
This system may be rewritten using matrix-notation. Indeed, set
![]() ,
,
then the above system is equivalent to the matricial equation
![]() .
.
Using the matrix product, we get
![]() .
.
The matrix
![]()
is called the coefficient matrix of the system. Note that the coefficients of the matrix A can be constant or not. The vector function
![]()
is called the nonhomogeneous term.
Remark: One may think that the equation above is only valid for linear systems of two equations. However, that is not the case. For example, consider the linear system
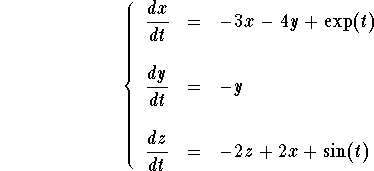
Then, in matricial notation, the system is equivalent to
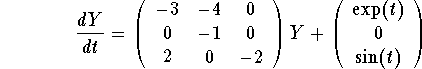 ,
,
where
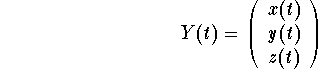 .
.
Consider the homogeneous linear system
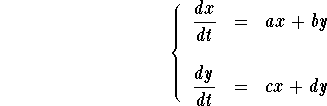
The equilibrium points are given by the equations
![]()
Clearly, x=0 and y=0 give a trivial solution. Hence, the function
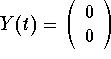 gives a constant solution to the linear system. We call it the
trivial solution. In general, the equilibrium points are the
intersection between two lines. Since the two lines intersect,
they are the same (if parallel) or the intersection is reduced to
one point. So, the set of equilibrium points is the entire line
ax+by=0, or the trivial point (0,0). This conclusion is related to
the determinant of the matrix coefficient. Indeed, if
gives a constant solution to the linear system. We call it the
trivial solution. In general, the equilibrium points are the
intersection between two lines. Since the two lines intersect,
they are the same (if parallel) or the intersection is reduced to
one point. So, the set of equilibrium points is the entire line
ax+by=0, or the trivial point (0,0). This conclusion is related to
the determinant of the matrix coefficient. Indeed, if
![]()
is not equal to 0 (zero), then we have one equilibrium point (the trivial one).
This is may be the most important property for linear systems. Consider the homogeneous linear system
![]() ,
,
then
This clearly implies that if ![]() and
and ![]() are two solutions and
are two solutions and ![]() and
and ![]() are two arbitrary constants, then
are two arbitrary constants, then
![]()
is also a solution. This conclusion is also known as the Principle of Superposition.
Clearly, from the Principle of Superposition, we may generate plenty
of solutions once two solutions are known. The natural question to
ask therefore, is whether we have obtained all the solutions. In
order to better appreciate this problem let's consider the following example.
Example: Consider the linear system
![]()
Show that any solution Y to this system is given as
![]() ,
,
where
![]()
and ![]() and
and ![]() are two constants.
are two constants.
Answer: It is easy to check that indeed ![]() and
and ![]() are solutions to the given system. Let Y be any solution. Set
are solutions to the given system. Let Y be any solution. Set
![]() .
.
By the uniqueness and existence theorem, Y is the only solution to the IVP
![]() .
.
Let us find ![]() and
and ![]() such that
such that ![]() . If this is the case, we should have
. If this is the case, we should have ![]() , which gives
, which gives
![]() ,
,
which implies
![]()
Clearly, this gives
![]() .
.
Consider the function
![]() .
.
The linearity principle implies that ![]() is a solution. And, since
is a solution. And, since
![]() ,
,
the uniqueness and existence theorem implies that in fact ![]() gives the desired conclusion.
gives the desired conclusion.
Remark: When you look at the above example you will notice that what made the conclusion work is that we were able to solve the algebraic system
![]()
and this was possible because the two vectors
![]()
are linearly independent. In fact, the above conclusion is always valid whenever we have a linear independence around.
![]() .
.
Assume that the vectors ![]() and
and ![]() are linearly independent. Then, the solution to the IVP
are linearly independent. Then, the solution to the IVP
![]() ,
,
is given by
![]() ,
,
for some constants ![]() and
and ![]() . In this case, the two-parameter family
. In this case, the two-parameter family
![]() ,
,
where ![]() and
and ![]() are arbitrary constants, is called the general solution of the system. Then, the two solutions
are arbitrary constants, is called the general solution of the system. Then, the two solutions ![]() and
and ![]() are said to be linearly independent.
are said to be linearly independent.
Example: Consider the undamped harmonic oscillator
![]() .
.
Show that any solution x is given by
![]() .
.
Answer: Consider the associated linear system
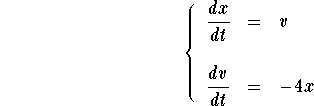
Set 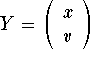 . Note that the second component is just the derivative of the first one. Consider the two vector functions
. Note that the second component is just the derivative of the first one. Consider the two vector functions
![]()
It is easy to check that these two vector functions are in fact solutions to the given system. Also, you may check that the two vectors
![]()
are linearly independent. Therefore, any solution Y of the system is given by
![]() ,
,
where ![]() and
and ![]() are two constants. Using the first component of Y, we see that any solution x(t) of the equation is given by
are two constants. Using the first component of Y, we see that any solution x(t) of the equation is given by
![]() ,
,
where ![]() and
and ![]() are two arbitrary constants.
are two arbitrary constants.
Clearly, the main problem now is how to find the two linearly independent solutions. This problem will be discussed in the next section and will use the eigenvalue and eigenvector technique.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Mohamed Amine Khamsi