Systems with Zero as an Eigenvalue
Systems with Zero as an Eigenvalue
We discussed the case of system with two distinct real eigenvalues,
repeated (nonzero) eigenvalue, and complex eigenvalues. But we did not
discuss the case when one of the eigenvalues is zero. In fact, it is
easy to see that this happen if and only if we have more than one
equilibrium point (which is (0,0)). In this case, we will have a
line of equilibrium points (the direction vector for this line is the
eigenvector associated to the eigenvalue zero).
Example. Find the general solution to
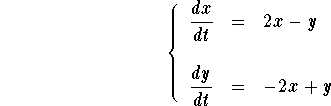
Answer. The characteristic polynomial of this system is
which reduces to 
. The eigenvalues are
and 
. Let us find the associated
eigenvectors.
, set
The equation 
translates into
The two equations are the same. So we have y = 2x. Hence an eigenvector is
, set
The equation 
translates into
The two equations are the same (as -x-y=0). So we have y = -x. Hence an eigenvector is
Therefore the general solution is
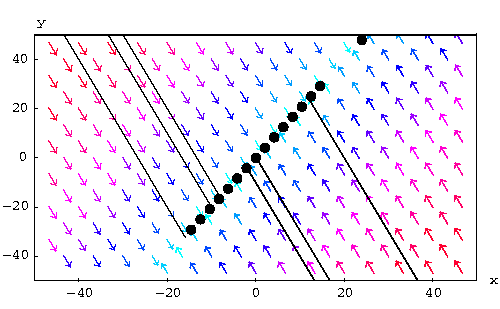
Note that all the solutions are line parallel to the vector
.
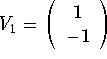When 
, the trajectory goes to infinity. But
when 
, the trajectory converge to the
equilibrium point on the line of equilibrium points (that is passing
by (0,0) and having 
as a direction vector). The picture below
explains more what is happening.
|
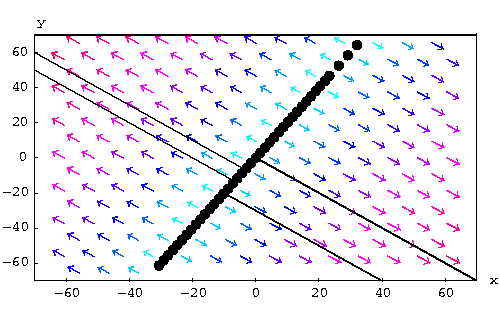
The general case is very similar to this example. Indeed, assume that
a system has 0 and 
as eigenvalues. Hence if is
an eigenvector associated to 0 and 
an eigenvector associated to
, then the general solution is
We have two cases, whether 
or 
.
, then 
is an equilibrium point.
, then the solution is a line parallel
to the vector . Moreover, we have when
, the solution tends away from the
line of equilibrium;
|
, the solution tends to the
equilibrium point 
along a line parallel to .
|
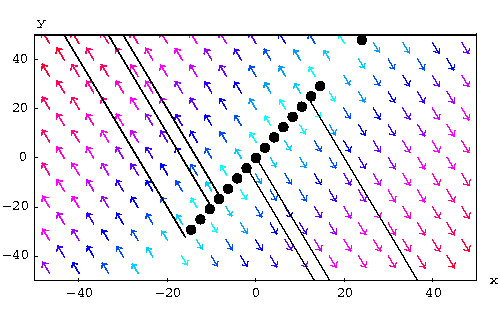
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author: Mohamed Amine Khamsi