 Repeated Eigenvalues
Repeated Eigenvalues Repeated Eigenvalues
Repeated Eigenvalues

Consider the linear homogeneous system
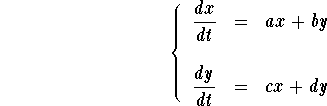
In order to find the eigenvalues consider the Characteristic polynomial
![]()
In this section, we consider the case when the above quadratic
equation has double real root (that is if ![]() )
the double root (eigenvalue) is
)
the double root (eigenvalue) is
![]()
In this case, we know that the differential system has the straight-line solution
![]()
where ![]() is an eigenvector associated to the eigenvalue
is an eigenvector associated to the eigenvalue
![]() . We also know that the general solution (which describes all
the solutions) of the system will be
. We also know that the general solution (which describes all
the solutions) of the system will be
![]()
where ![]() is another solution of the system which is linearly
independent from the straight-line solution
is another solution of the system which is linearly
independent from the straight-line solution ![]() . Therefore, the problem in this case is to find
. Therefore, the problem in this case is to find ![]() .
.
Search for a second solution.
Let us use the vector notation. The system will be written as
![]()
where A is the matrix coefficient of the system. Write
![]()
The idea behind finding a second solution ![]() , linearly independent
from
, linearly independent
from ![]() , is to look for it as
, is to look for it as
![]()
where ![]() is some vector yet to be found. Since
is some vector yet to be found. Since
![]()
and
![]()
(where we used ![]() ), then (because
), then (because ![]() is a solution of
the system) we must have
is a solution of
the system) we must have
![]()
Simplifying, we obtain
![]()
or
![]()
This equation will help us find the vector ![]() . Note that the
vector
. Note that the
vector ![]() will automatically be linearly independent from
will automatically be linearly independent from ![]() (why?).
This will help establish the linear independence of
(why?).
This will help establish the linear independence of ![]() from
from
![]() .
.
Example. Find two linearly independent solutions to the linear system
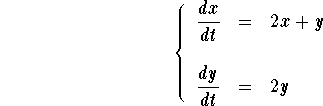
Answer. The matrix coefficient of the system is
![]()
In order to find the eigenvalues consider the Characteristic polynomial
![]()
Since ![]() , we have a repeated
eigenvalue equal to 2. Let us find the associated eigenvector
, we have a repeated
eigenvalue equal to 2. Let us find the associated eigenvector ![]() . Set
. Set
![]()
Then we must have ![]() which translates into
which translates into
![]()
This reduces to y=0. Hence we may take
![]()
Next we look for the second vector ![]() . The equation giving this
vector is
. The equation giving this
vector is ![]() which translates into the
algebraic system
which translates into the
algebraic system
![]()
where
![]()
Clearly we have y=1 and x may be chosen to be any number. So we take x=0 for example to get
![]()
Therefore the two independent solutions are
![]()
The general solution will then be
![]()
Qualitative Analysis of Systems with Repeated Eigenvalues
Recall that the general solution in this case has the form
![]()
where ![]() is the double eigenvalue and
is the double eigenvalue and ![]() is the associated
eigenvector. Let us focus on the behavior of the solutions when
is the associated
eigenvector. Let us focus on the behavior of the solutions when ![]() (meaning the future). We have two cases
(meaning the future). We have two cases
![]()
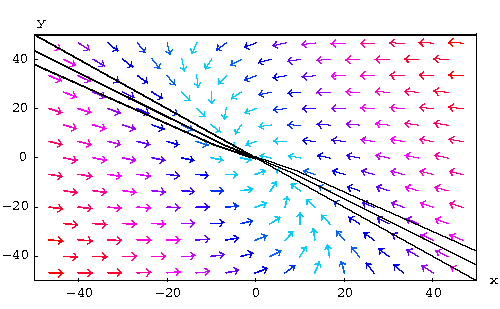
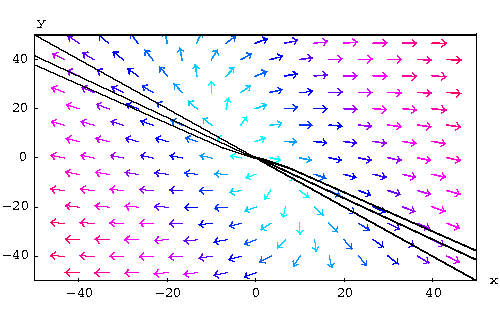
In this case, the equilibrium point (0,0) is a sink. On the other hand, when t is large, we have
![]()
So the solutions tend to the equilibrium point tangent to the
straight-line solution. Note that is ![]() , then the solution is
the straight-line solution which still tends to the equilibrium
point.
, then the solution is
the straight-line solution which still tends to the equilibrium
point.
|
|
Another example of the repeated eigenvalue's case is given by harmonic oscillators.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Mohamed Amine Khamsi