 Eigenvalues and Eigenvectors Technique
Eigenvalues and Eigenvectors Technique Eigenvalues and Eigenvectors Technique
Eigenvalues and Eigenvectors Technique

In this section we will discuss the problem of finding two linearly independent solutions for the homogeneous linear system
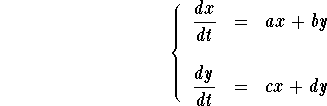
Let us first start with an example to illustrate the technique we will be developping.
Example: Draw the direction field of the linear system
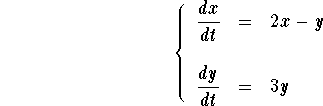
Answer: The following is the direction field:
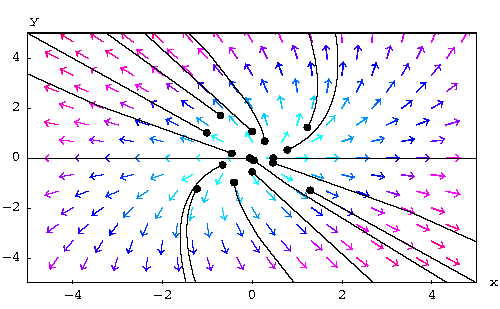
|
Remark: From the above example we notice that some solutions
lie on straight lines (can you spot them?). So it is natural to investigate whether and when an homogeneous linear system has solutions which are straight-lines.
Consider the homogeneous linear system (in the matricial notation)
![]()
A straight-line solution is a vector function of the form
![]() ,
,
where ![]() is a constant vector not equal to the zero vector
is a constant vector not equal to the zero vector ![]() . The vector
. The vector ![]() is the direction vector of the line on which the solution lives. Keep in mind that the solutions of the system may describe trajectories of moving objects. So, in this case, we may think of it as an object moving along a straight line.
is the direction vector of the line on which the solution lives. Keep in mind that the solutions of the system may describe trajectories of moving objects. So, in this case, we may think of it as an object moving along a straight line.
Remark: Note that if Y(t) is a straight-line solution, then ![]() is also a straight-line solution.
is also a straight-line solution.
Clearly, we have
![]() .
.
Therefore, we have
![]() .
.
Since ![]() and
and ![]() are constant vectors, we deduce that
are constant vectors, we deduce that ![]() is a constant function. Denote it by
is a constant function. Denote it by
![]()
Clearly, this is a first order differential equation which is linear as well as separable. Its solution is
![]() ,
,
where C is an arbitrary constant. So, if a straight-line solution exists, it must be of the form
![]() ,
,
where C is an arbitrary constant, and ![]() is a non-zero constant vector which satisfies
is a non-zero constant vector which satisfies
![]()
Note that we don't have to keep the constant C (read the above remark).
Let us illustrate the above ideas with an example.
Example: Find any straight-line solution to the system
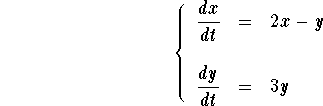
Answer: First, let us find the constant vector
![]()
such that ![]() for some
for some ![]() . Easy computations give
. Easy computations give
![]()
We have two cases:
![]() .
.
We may ignore the constant ![]() (see the above remark). Therefore, the solution
(see the above remark). Therefore, the solution
![]()
is a straight-line solution to the system.
![]() .
.
We may again ignore the constant ![]() . Hence, the solution
. Hence, the solution
![]()
is a straight-line solution to the system.
![]()
Are these the only straight-lines? The answer is: "yes," but this will be discussed later.
![]()
Any straight-line solution may be found in the form
![]() ,
,
where ![]() is a non-zero constant vector which satisfies
is a non-zero constant vector which satisfies
![]()
The constant ![]() is called an eigenvalue of the matrix A, and
is called an eigenvalue of the matrix A, and ![]() is called an eigenvector associated to the eigenvalue
is called an eigenvector associated to the eigenvalue ![]() of the matrix A. Clearly, if
of the matrix A. Clearly, if ![]() is an eigenvector associated to
is an eigenvector associated to ![]() , then
, then ![]() is also an eigenvector associated to
is also an eigenvector associated to ![]() . Our next target is to find out how to search for the eigenvalues and eigenvectors of a matrix.
. Our next target is to find out how to search for the eigenvalues and eigenvectors of a matrix.
![]()
and assume that ![]() is an eigenvalue of A. Then there must exist a non-zero vector
is an eigenvalue of A. Then there must exist a non-zero vector 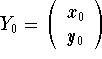 , such that
, such that ![]() . This equation may be rewritten as the algebraic system
. This equation may be rewritten as the algebraic system
![]()
which is equivalent to the system
![]()
Since both ![]() and
and ![]() can not be equal to zero at the same time, we must have the determinant of the system equal to zero. That is,
can not be equal to zero at the same time, we must have the determinant of the system equal to zero. That is,
![]() ,
,
which reduces to the algebraic equation
![]() .
.
Note that the above equation is independent of the vector ![]() . This equation is called the Characteristic Polynomial of the system.
. This equation is called the Characteristic Polynomial of the system.
Example: Find the characteristic polynomial and the eigenvalues of the matrix
![]()
Answer: The characteristic polynomial is given by
![]() .
.
This is a quadratic equation. Its only roots are ![]() and
and ![]() . These are the eigenvalues of the matrix.
. These are the eigenvalues of the matrix.
Assume ![]() is an eigenvalue of the matrix A. An eigenvector
is an eigenvalue of the matrix A. An eigenvector ![]() associated to
associated to ![]() is given by the matricial equation
is given by the matricial equation
![]() .
.
Set 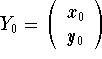 . Then, the above matricial equation reduces to the algebraic system
. Then, the above matricial equation reduces to the algebraic system
![]()
which is equivalent to the system
![]()
Since ![]() is known, this is now a system of two equations and two unknowns. You must keep in mind that if
is known, this is now a system of two equations and two unknowns. You must keep in mind that if ![]() is an eigenvector, then
is an eigenvector, then ![]() is also an eigenvector.
is also an eigenvector.
Example: Consider the matrix
![]() .
.
Find all the eigenvectors associated to the eigenvalue ![]() .
.
Answer: In the above example we checked that in fact ![]() is an eigenvalue of the given matrix. Let
is an eigenvalue of the given matrix. Let ![]() be an eigenvector associated to the eigenvalue
be an eigenvector associated to the eigenvalue ![]() . Set
. Set 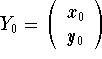 . Then we must have
. Then we must have
![]()
which reduces to the only equation
![]() ,
,
which yields ![]() . Therefore, we have
. Therefore, we have
![]()
Note that we have all of the eigenvectors associated to the eigenvalue ![]() .
.
![]() , perform the following steps:
, perform the following steps:
![]() .
.
This is a quadratic equation which has one double real root, or two distinct real roots, or two complex roots.
![]() .
.
If you find a parameter factorized in front of ![]() , there will be no need to keep it;
, there will be no need to keep it;
![]() .
.
Remark: It is not hard to show that two straight-line solutions generated by two different eigenvalues are in fact linearly independent. Combined with the results of the previous section we now see how straight-lines may be used to help find the solutions of an homogeneous linear system. This technique is also related to the case of second order differential equation with constant coefficients. Indeed, consider the second order differential equation
![]() .
.
Set ![]() . Then the second order differential equation is equivalent to the first order system
. Then the second order differential equation is equivalent to the first order system
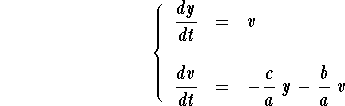
The matrix coefficient of the system is
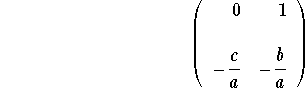 .
.
The characteristic polynomial is
![]() ,
,
which is equivalent to the equation
![]() .
.
We recognize the characteristic equation associated to the second order differential equation.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Mohamed Amine Khamsi