 The Wronskian
The Wronskian  The Wronskian
The Wronskian
Let ![]() and
and ![]() be two differentiable functions. We will say that
be two differentiable functions. We will say that
![]() and
and ![]() are proportional if and only if there exists a
constant C such that
are proportional if and only if there exists a
constant C such that ![]() . Clearly any function is
proportional to the zero-function. If the constant C is not
important in nature and we are only interested into the proportionality
of the two functions, then we would like to come up with an equivalent
criteria. The following statements are equivalent:
. Clearly any function is
proportional to the zero-function. If the constant C is not
important in nature and we are only interested into the proportionality
of the two functions, then we would like to come up with an equivalent
criteria. The following statements are equivalent:
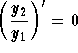 ;
;
Therefore, we have the following:
Define the Wronskian ![]() of
of ![]() and
and ![]() to be
to be ![]() , that is
, that is
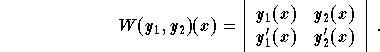
The following formula is very useful (see reduction of order technique):
![]()
Remark: Proportionality of two functions is equivalent to their linear dependence. Following the above discussion, we may use the Wronskian to determine the dependence or independence of two functions. In fact, the above discussion cannot be reproduced as is for more than two functions while the Wronskian does....