 Riccati Equations
Riccati Equations

Before we give the formal definition of Riccati equations,
a little introduction may be helpful.
Indeed, consider the first order differential equation
If we approximate f(x,y), while x is kept constant, we will get
If we stop at y, we will get a linear equation.
Riccati looked at the approximation to the second degree: he considered equations of the type
These equations bear his name, Riccati equations. They are nonlinear and
do not fall under the category of any of the classical equations.
In order to solve a Riccati equation, one will need a particular solution.
Without knowing at least one solution, there is absolutely no chance to find any
solutions to such an equation. Indeed, let y1 be a particular solution of
Consider the new function z defined by
Then easy calculations give
which is a linear equation satisfied by the new function z. Once it is solved, we go back to y via the relation
Keep in mind that it may be harder to remember the above equation satisfied by z. Instead, try to do the calculations whenever you can.
Example. Solve the equation
knowing that y1 = 2 is a particular solution.
Answer. We recognize a Riccati equation. First of all we need to make sure
that y1 is indeed a solution. Otherwise, our calculations will be fruitless.
In this particular case, it is quite easy to check that y1 = 2 is a solution. Set
Then we have
which implies
Hence, from the equation satisfied by y, we get
Easy algebraic manipulations give
Hence
z' = -3z -1.
This is a linear equation. The general solution is given by
Therefore, we have
Note: If one remembers the equation satisfied by z,
then the solutions may be found a bit faster. Indeed in this example, we have P(x) = -2, Q(x) = -1, and R(x) = 1. Hence the linear equation satisfied by the new function z, is
Example. Check that
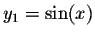 is a solution to
is a solution to
Then solve the IVP
We will let the reader check that 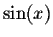 is indeed a particular solution of the given differential equations.
We also recognize that the equation is of Riccati type. Set
is indeed a particular solution of the given differential equations.
We also recognize that the equation is of Riccati type. Set
which gives
Hence
Substituting into the equation gives
Easy algebraic manipulations give
Hence
This is the
linear equation satisfied by z. The integrating factor is
The general solution is
Now it is time to go back to the original function y. We have
The initial condition y(0) = -1 implies 1/C = -1, or C = -1. Therefore the solution to the IVP is

[Differential Equations]
[Algebra]
[Trigonometry ]
[Calculus]
[Complex Variables]
[Matrix Algebra]
 S.O.S. MATHematics home page
S.O.S. MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: Mohamed
Amine Khamsi
Last Update 9-15-98
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Riccati Equations
Riccati Equations  Riccati Equations
Riccati Equations 
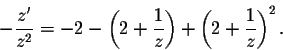
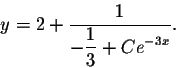
![]() is a solution to
is a solution to
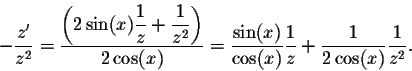
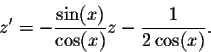
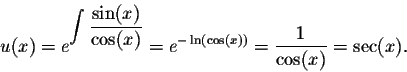
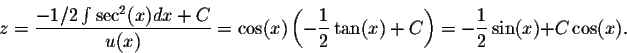
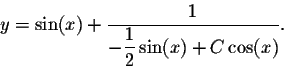
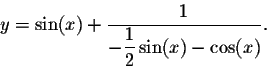

 S.O.S. MATHematics home page
S.O.S. MATHematics home page 