Introduction and First Definitions
- 1.
- A differential equation is an equation involving an unknown
function and its derivatives.
- 2.
- The order of the differential equation is the order of the
highest derivative of the unknown function involved in the equation.
- 3.
- A linear differential equation of order n is a
differential equation written in the following form:
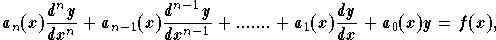
where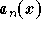 
is not the zero function. Note that some may use the
notation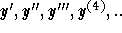 
for the derivatives.
A linear equation obliges the unknown function y to have some
restrictions. Indeed, the only operations which are accepted for the
variable y are:
- (i)
- Differentiating y;
- (ii)
- Multiplying y and its derivatives by a function of the
variable x
- (iii)
- Adding what you obtained in (ii) and let it be equal to a
function of x.
- 4.
- Existence: Does a differential equation have a
solution?
- 5.
- Uniqueness: Does a differential equation have more
than one solution? If yes, how can we find a solution which satisfies
particular conditions?
- 6.
- A problem in which we are looking for the unknown function
of a differential equation where the values of the unknown function
and its derivatives at some point are known is called an initial
value problem (in short IVP).
- 7.
- If no initial conditions are given, we call the description of all
solutions to
the differential equation the general solution.
[Differential Equations]
[First Order D.E.]
[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Complex Variables]
[Matrix Algebra]
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
Author: Mohamed
Amine Khamsi
Last Update 6/22/98
Copyright © 1999-2023 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour