-
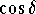 .
.
Answer: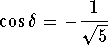 .
.
-
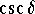 .
.
Answer: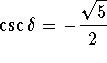 .
.
-
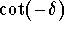 .
.
Answer: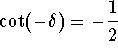 .
.
-
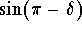 .
.
Answer: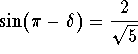 .
.
Answer: The angle is approximately ![]() .
.
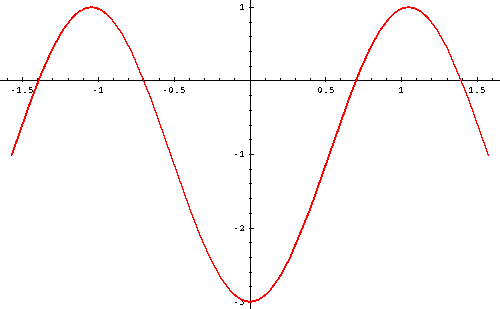
|
Answer: The values are:
- a=-2.
- b=3.
-
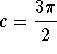 .
. - d=-1.
Answer: Let x be the number of
Doberman pinschers, and y be the number of German shepherds. The system of inequalities is:

Answer: The angles are ![]() , and
, and ![]() .
.
![]()
Answer:
![]()
- Convert z to its trigonometric form.
Answer: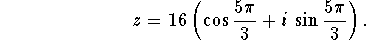
- Using DeMoivre's theorem, write
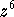 as a complex number
in standard form (a + bi).
as a complex number
in standard form (a + bi).
Answer: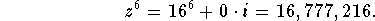
- Use DeMoivre's theorem to solve the equation

Write your solutions in standard form.
Answer: The answers are: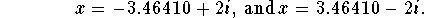
![]()
Show all steps.
Answer:
![]()
![]()
- Eliminate the parameter and obtain a rectangular equation for
the graph described by x and y above.
Answer: The equation is: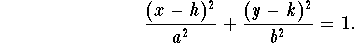
- Using you observations from the problem above, find a set of
parametric equations for the ellipse with vertices at (4,7) and
(4,-3), and foci at (4,5) and (4,-1).
Answer: The set of parametric equations is
Answer:
|
![]()
Answer: The formula for finding the sum of an infinite
geometric sequence is ![]() . In this case a=7 and r=-3/7; thus the sum of the given
sequence is
. In this case a=7 and r=-3/7; thus the sum of the given
sequence is 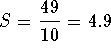
Answer: There are four solutions:
![]()
- In how many ways can the 4 be chosen?
Answer: The 4 employees can be chosen in 495 different ways. - In how many ways can 4 of the 12 employees be chosen to be
placed in 4 different jobs, if they are all well qualified for any of
the 4 positions?
Answer: The 4 employees can be chosen in 11880 different ways.
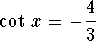 , and
, and 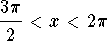 ,
find exact values for the following:
,
find exact values for the following:
-
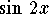 .
.
Answer: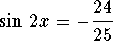 .
.
-
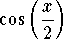 .
.
Answer: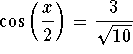 .
.
-
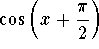 .
.
Answer: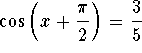 .
.
![]()
Answer: The nth term has the form
![]()
Answer: The equation of the tangent line is
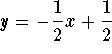 .
.
Answer: The unit vector is
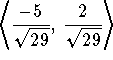 .
.
![]()
Answer:
- When n=1, the formula is valid, because
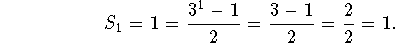
- Assuming that
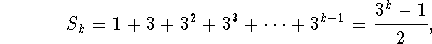
You must show that

To do this, write the following:
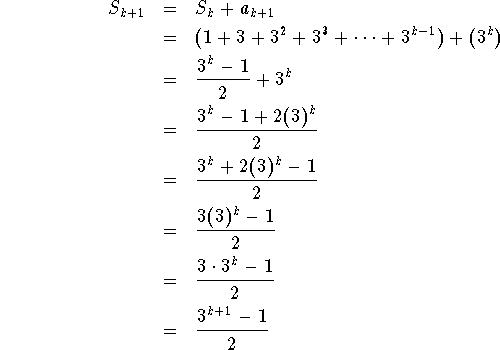
Combining the results from the two parts, it is concluded by mathematical induction that the formula is valid for every positive integer.