-
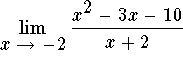
Answer: -7
-
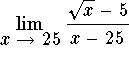
Answer:
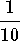
-
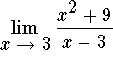
Answer: diverges
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Answer:
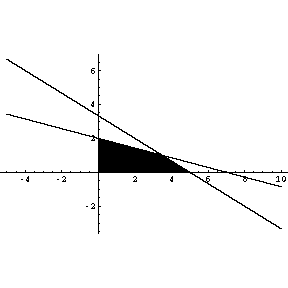
Corner points: (0.0), (0,2), (5,0) and ![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Answer:
Evaluate z at the corner points: (4,0), (12,0) and (6,4)
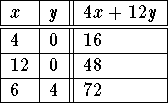
Minimum: z= 16
-
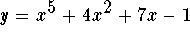
Answer:
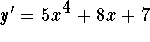
-
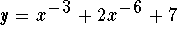
Answer:
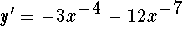
-
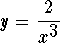
Answer:
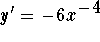
-
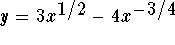
Answer:
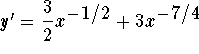
-
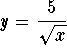
Answer:
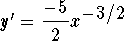
Answer:
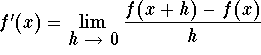
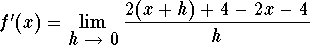
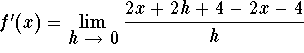
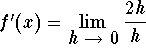
f'(x)= 2
f'(3)=2
- Find the marginal cost C'(x)
Answer: C'(x)=12x
- Find and interpret C'(500)
Answer: C'(500)=6000
Approximately the cost of the 501st pizza.
- Find the exact cost to produce the 501st pizza.
Answer: C(501)-C(500) = 6,006
- How are the answers in b and c related?
Answer: b approximates c
- A candy company has 300 kilograms of chocolate-covered nuts and 100
kilograms of chocolate covered raisins to be sold as two different
mixes. One mix will contain 1/2 nuts and 1/2 raisins and will sell for $4 per kilogram. The other will contain 3/4 nuts and 1/4 raisins and will sell
for $6.50 per kilogram. How many kilograms of each mix should the
company prepare for maximum revenue?
Answer:
Maximize r = 4x +6.5y
x=# of kilograms of
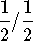 mix
mix
y=# of kilograms of
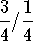 mix
mix
Subject to
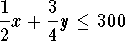
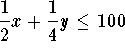
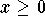
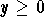
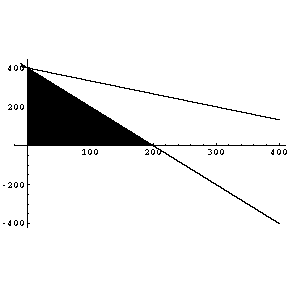
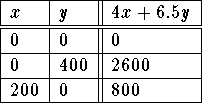
The company should make 400kg of the
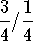 mix
mix
- A bakery makes both cakes and cookies. Each batch of cakes
requires 2 hours in the oven and 3 hours in the decorating room. Each
batch of cookies needs 1 and a half hours in the oven and 2/3 of an
hour in the decorating room. The oven is available no more than 15
hours a day while the decorating room can be used no more than 13
hours a day. How many batches of cakes and cookies should the bakery
make in order to maximize profits if cookies produce a profit of $20
per batch and cakes produce a profit of $30 per batch?
Answer:
Maximize 30x+20y
x =# of batches of cake
y =# of batches of cookies
Subject to
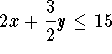
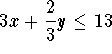
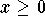
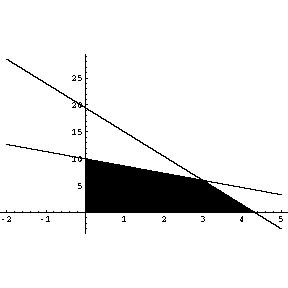
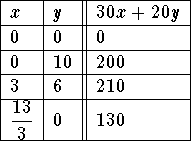
The bakery should make 3 batches of cake and 6 batches of cookies.
