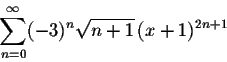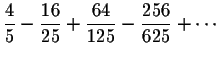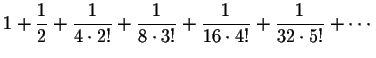Practice Exam: Series and Taylor Series
Practice Exam: Series and Taylor Series
Time: 60 minutes
Problem 1 (15 points)
Use the fourth degree Taylor polynomial of 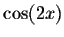 to find the exact value of
Explain your reasoning!
to find the exact value of
Explain your reasoning!
Problem 2 (15 points)
Find the third degree Taylor polynomial of
with center x0=3
.
Problem 3 (15 points)
Let
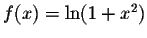 . Find the Taylor series of f
. Find the Taylor series of f(
x)
with center x0=0
and its radius of convergence.
Problem 4 (15 points)
Find the radius of convergence of the power series
Problem 5 (20 points)
Find the exact value of the following series:
Problem 6 (20 points)
An antibiotic decays exponentially in the human body with a half-life of about 2.5 hours. Suppose a patient takes a 250 mg tablet of the antibiotic every 6 hours.
- 1.
- Write an expression for Q2, Q3, Q4, where Qn is the amount (in mg) of the antibiotic in the body after the
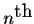 tablet is taken. Note that Q1=250 mg.
tablet is taken. Note that Q1=250 mg.
- 2.
- Write an expression for Qn, and put it in closed form.
- 3.
- Assume the antibiotic treatment consists of a total of 28 tablets. Give a numerical estimate for the amount of antibiotic in the body immediately after the patient takes the last tablet of the treatment.
If you would like to check your answers, click on Answer.
[Calculus]
[CyberExam]
 S.O.S MATH: Home Page
S.O.S MATH: Home Page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Helmut Knaust
 Practice Exam: Series and Taylor Series
Practice Exam: Series and Taylor Series