| Answers. |
|---|
Problem 1. Find the limit
![]()
Answer. Note that we have an indeterminate form ![]() . You may want to try Hopital rule and see how difficult
the calculations become except if you use the substitution
. You may want to try Hopital rule and see how difficult
the calculations become except if you use the substitution ![]() .
Here we will use Taylor Polynomials to find this limit. We have
.
Here we will use Taylor Polynomials to find this limit. We have
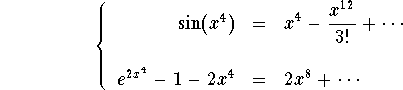
This gives
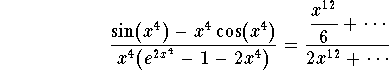
Clearly the limit is
![]()
Problem 2. Find the limit
![]()
Answer. Note that we have an indeterminate form ![]() . Since we a have a square root in the function, we will use
the conjugate forms to get rid of it. We have
. Since we a have a square root in the function, we will use
the conjugate forms to get rid of it. We have
![]()
Since

(note that |x| = -x because ![]() and therefore x
< 0), hence
and therefore x
< 0), hence
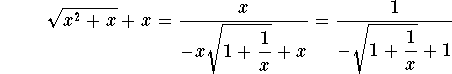
It is now obvious that
![]()
Problem 3. Find
![]()
Answer. Note that we have an indeterminate form ![]() . In
order to find the limit, we will use the formula
. In
order to find the limit, we will use the formula
![]()
We can assume that ![]() . In this case, we have
. In this case, we have
![]()
Since
![]()
we have to concentrate on the term ![]() . We have
. We have
![]()
Since
![]()
we get
![]()
Therefore we have
![]()
Problem 4. Determine the convergence or divergence of
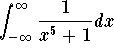
Answer. The bad points are ![]() ,
, ![]() , -1.
, -1.
At ![]() , we have
, we have
![]()
when ![]() . Recall that
. Recall that
![]()
when ![]() if and only if
if and only if
![]()
Using the limit test and the p-test, we know that
![]()
are both convergent. Thereofre
![]()
are both convergent.
At -1, we have
![]()
when ![]() . Again using the limit test and the
p-test, we know that
. Again using the limit test and the
p-test, we know that
![]()
is divergent. Therefore the improper integral
![]()
is divergent.
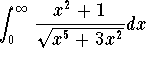
Answer. The bad points are 0 and ![]() .
.
At ![]() , we have
, we have
![]()
when ![]() . Using the limit test and the
p-test, we know that
. Using the limit test and the
p-test, we know that
![]()
is divergent. Therefore
![]()
is divergent. So the improper integral
![]()
is divergent. We suggest to consider the other bad points too though
there is no need for that. But you never know, your previous conclusion may
be wrong!!!!
At 0, we have
![]()
when ![]() . Using the limit test and the
p-test, we know that
. Using the limit test and the
p-test, we know that
![]()
is divergent. Therefore
![]()
is divergent. So again we get the divergence of the hole improper integral.
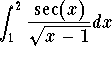
Answer. The bad points are 1 and ![]() .
.
At 1, we have
![]()
when ![]() . Using the limit test and the
p-test, we know that
. Using the limit test and the
p-test, we know that
![]()
is convergent.
At ![]() , we have
, we have
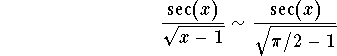
when ![]() . And since
. And since
![]()
when ![]() and the improper integral
and the improper integral
![]()
is divergent, then using the limit test and the p-test, we have
![]()
is divergent. We deduce then that the improper integral
![]()
is divergent.
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour