Taylor Polynomials
Taylor Polynomials
The derivative of f(t) is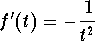 
, thus 
.
Since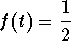 
, we obtain as an equation for the tangent line at 
:
One way to see that the tangent line to a function f(x) at
a given point 
is the best line approximating the function is to observe that the tangent line is the (only) line
passing through the point 
and having the same slope as f(x) at .
So what about about finding the "best'' parabola approximating the function f(x) near ? We should look for the parabola passing through , which has the same slope (the first derivative) as f(x) at , and which has the same second derivative as f(x) at !
Let's try it: Consider 
near 
.
The parabola we are trying to find has the generic form:
Writing the parabola this way, it is easier to compute its derivatives at : p'(x)=b +2 c (x-1) and p''(x)=2 c. Substituting we obtain:
Recall, we want to find the parabola which has the same derivatives at as f(x). This yields the conditions:
Now 
; 
and 
.
Solving for the coefficients and substituting in the formula for p(x), we obtain
The polynomial p(x) is called the second degree Taylor polynomial
of the function at the point .
The picture below shows f(x) in black and its second degree Taylor polynomial at in red.
 |
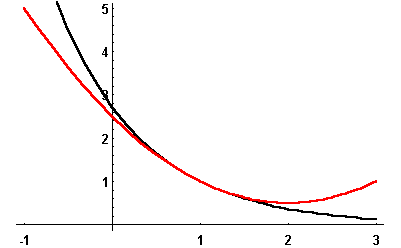It is not hard to see what the general formula will look like: If we replace by a "general'' above, we obtain:
as the general form of the Taylor polynomial at ;
We need that
and consequently
is called the center of the Taylor polynomial. Note: The center is fixed, the variable name for the polynomial is x. Even if we consider the same function f(x),
different centers will usually yield different Taylor polynomials (just as a function usually has different tangent lines at various points!).
with the center 
.
Click here for the answer, or to continue.