Introduction to Series

The notion of series is closely related to the sum of numbers. In fact, whenever one hears the word series, the first thing to come to mind is the sum of numbers. This is the basic difference between series and sequences. So series, as we will see, are here to help us add numbers. So what is the problem? Let us do a simple addition problem. Let me give 3 numbers: A, B and C. If I ask you to add them, you will take a pen and a paper or a calculator and do the following:

1.

You will enter the number A, then

2.

You will add to it the number B, to get

3.

And finally, you will add C to the previous result to get

So, if you are given one million numbers, you will still enter one by one to add all of them. A very simple operation, isn't it? Now what would happen if you were given infinitely many numbers? What would you do?

Example: Add the numbers .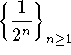

Answer: First we enter (into our calculator) the number . The output will be

.

Then we add to it the next number on the list to get

.

Again we add to it the next number on the list

.

We keep on doing this to get

,

etc... For example, we have

.

So you will jump and say: Oh the numbers are getting closer and closer to 1. We will see (in geometric series) that your answer is correct. But we should not trust this kind of conclusion in general. We should be always ready to check our conclusions.

The above example helps us to see how a person may add infinitely many numbers. Indeed, let be a sequence of numbers (which we are trying to add). Set

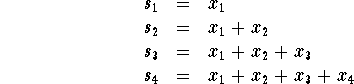
and for , we have

.

The new sequence is called the sequence of partial sums. These are the numbers one will see on the screen of his or her calculator. Any conclusion to the total sum of the given numbers will be made subject to our observation of this sequence.

In order to make a difference between a given sequence which we may or not be interested into adding its numbers, we introduce a new notation which carries the problem we discussed above. The new symbol will be used since it is very close to the meaning we are trying to reach, that is, the sum of numbers. The notation commonly used for a series is

and we will call it the series .

Remark: Remember that for a given series , we naturally associate the sequence of partial sums defined by

.

[Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour