 Bertrand Series
Bertrand Series Bertrand Series
Bertrand Series

The Bertrand series are defined as
![]() ,
,
where ![]() and
and ![]() are real numbers. For example, the series
are real numbers. For example, the series
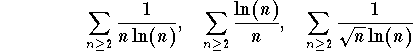 ,
,
are Bertrand series. Here we will discuss the convergence and divergence of such series.
First, note that if ![]() , then the sequence
, then the sequence 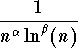 is not bounded. Hence, it will not tend to 0, and therefore the series
is not bounded. Hence, it will not tend to 0, and therefore the series
![]() ,
,
is divergent. So, we will assume ![]() .
.
We have three cases:
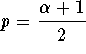 . Hence, we have
. Hence, we have ![]() .
.
Since ![]() , we get
, we get
![]() .
.
So, for some ![]() , we have
, we have
![]() ,
,
which implies
![]() .
.
By the p-test we know that the series ![]() is divergent (since p <1). The Basic Comparison Test implies that the series
is divergent (since p <1). The Basic Comparison Test implies that the series
![]()
is divergent.
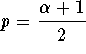 . Hence, we have
. Hence, we have ![]() .
.
Since ![]() , we get
, we get
![]() .
.
So, for some ![]() , we have
, we have
![]() ,
,
which implies
![]() .
.
By the p-test we know that the series ![]() is convergent (since p >1). The Basic Comparison Test implies that the series
is convergent (since p >1). The Basic Comparison Test implies that the series
![]()
is convergent.
![]() .
.
It is easy to check that for large x (more precisely ![]() ), the function f(x) is decreasing. We will easily prove then that
), the function f(x) is decreasing. We will easily prove then that
![]() ,
,
and
![]() ,
,
where M is an integer such that f(x) is decreasing on ![]() .
.
Note that if ![]() , then we have
, then we have
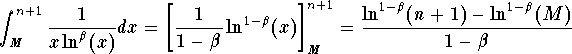 ,
,
and if ![]() (we may take M=2), then we have
(we may take M=2), then we have
![]() .
.
We have three cases:
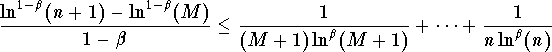 .
.
Since 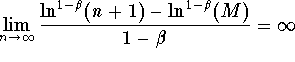 , then the series
, then the series 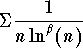 is not bounded,and therefore is divergent.
is not bounded,and therefore is divergent.
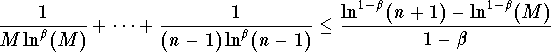 ,
,
but, since
![]() ,
,
for large n, we get
![]() ,
,
which means that the sequence of partial sums associated to the series
![]()
is bounded. Therefore, this series is convergent.
![]() ,
,
which implies
![]() .
.
Since
![]() ,
,
we conclude that the partial sums associated to the series
![]()
are not bounded. Therefore, this series is divergent.
Let us summarize the above conclusions regarding the Bertrand series
![]()
For example, we have
![]()
is divergent;

is divergent;

is convergent.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi