More on Limit of a SequenceMore on Limit of a Sequence
is not bounded, therefore it is divergent.
, for 
.
and 
are convergent and 
and 
are two arbitrary real numbers, then the new sequence 
is convergent. Moreover, we have
.
It is also true that the sequence 
is convergent and
.
is convergent and 
and 
for any 
, then the sequence 
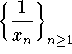is convergent. Moreover, we have
.
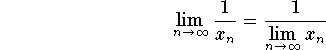The following examples will be useful to familiarize yourself with limit of sequences.
Example: Show that for any number a such that 0 < a <1, we have
.
Answer: Since 0 < a <1, then the sequence 
is obviously decreasing and bounded; hence it is convergent. Write
.
We need to show that L=0. We have
,
since the sequence 
is a tail of the sequence ; hence they have the same limit. But,
using the previous properties, we get
,
which implies
.
Since 
, then we must have L=0.
One may wonder, what happened to the sequence if a > 1? It is divergent since it is not bounded. This follows from
and
.
Remark: Note that it is possible to talk about a sequence of
numbers which converges to 
. Of
course, we do reserve the word convergent to sequences which converges
to a number; is not a number. The following shows the process:
converges to 
(or, to 
), if and only if, for any real number M > 0, there exists an integer 
, such that 
, we have 
(or 
).
In particular, if 
as 
and 
for any , then we have
A sequence which converges to is obviously not bounded.
For example, we have
for any a > 1.
Example: Show that the sequence
is convergent.
Answer: Note that
Hence, we have
.
So the sequence 
is bounded. Next, let n=1, we get
and if we let n=2, we get
You may convince yourself by computing the first numbers of the sequence so that they are decreasing. It is natural to check whether this is the case, so we need to compare the two numbers
,
for any . We have
.
Since
and
we get
,
which implies
.
This is exactly what we expected. Therefore, the sequence is decreasing. Since it is bounded, we conclude that it is convergent.
The next natural question to ask is: what is the limit of the sequence?
In the subsequent results we will show that in fact this sequence converges to 5.
Example: Show that
Answer: Since
then
.
Also, it is clear that 
for any . Putting the two results together, we conclude that 
is decreasing and bounded. Therefore, it is convergent. Let us write
.
We have 
, for any . Assume that 
. Then we have
which implies
for any . This is impossible since the sequence 
is not bounded (since 
). Therefore, we have L=1, that is,
In fact, we have
for any a > 0.
The next result is extremely useful. It is known as the Pinching
Theorem or the Sandwich Theorem:
Assume that the sequences
Then the sequence
. and are convergent and
. 
is convergent. Moreover, we have
.
Example: Show that
.
Answer: We have
In the above examples, we showed that
The above theorem implies the conclusion
.
Example: Discuss the convergence of
Answer: It is not an easy example. The reason is that 
behaves very badly when n gets large. But we will make use of the fact that is bounded and 
gets small when n gets large. We have
.
Since
then by the Pinching Theorem, we conclude that
.
This is a very simple example which shows how powerful the Pinching
Theorem is.
The next result is also useful and very commonly used.
belongs to the domain of f(x) and 
, as , then we have
Example: Since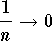 
, we have
a result we already proved in a harder way....
Example: Show that the sequence
is convergent and find its limit.
What do you think about
for any a > 0?
Next we will discuss some special limits.
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi