Power Series

is convergent exactly when -1<q<1.

Rename "q" to "x", and flip sides:

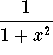when -1<x<1. We can rewrite the function as a series! Consider another example: What about rewriting tex2html_wrap_inline114 ? Rewrite:

and use the formula for the geometric series with :

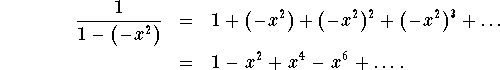
eqnarray22

Since the geometric series formula "works" for |q|<1, this series expansion will work exactly when , i.e., when |x|<1. (Check this carefully!!!)

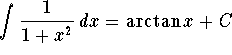Let's dream on, and integrate both sides: tex2html_wrap_inline124

, so we obtain:

If we plug in x=0 on both sides, using , we obtain C=0 and thus

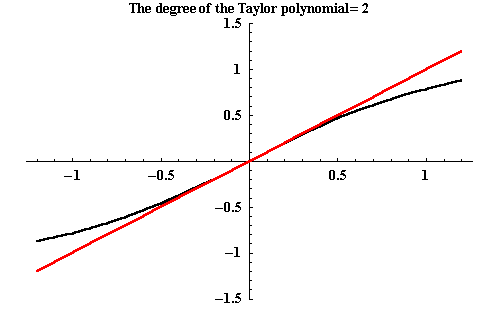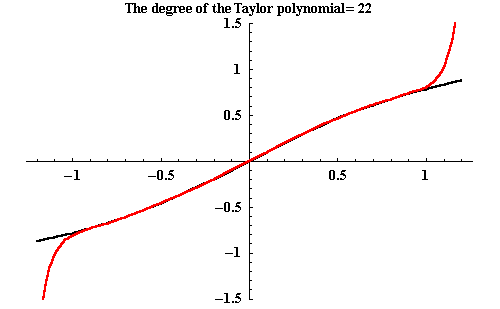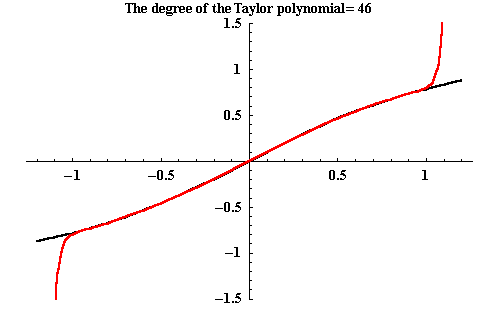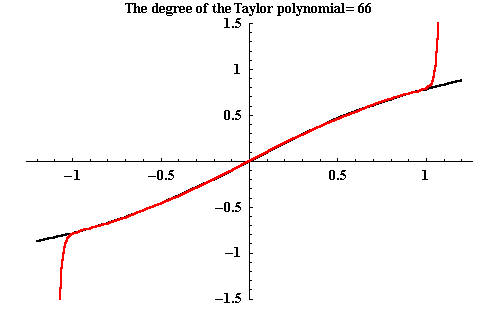
Let's check graphically whether this might work: The graph of is black, the sum of the first terms on the right are depicted in red. (The "number of terms" in the picture actually also counts the terms with zero coefficients!)

It seems to work as long as -1<x<1. With a little bit of work, the formula for the geometric series has led to a series expression for the inverse tangent function!

As it turns out, many familiar (and unfamiliar) functions can be written in the form

as an infinite sum of the product of certain numbers and powers of the variable x. Such expressions are called power series with center 0; the numbers are called its coefficients. Slightly more general, an expression of the form

is called a power series with center .

Using the summation symbol we can write this as

Try it yourself!

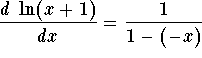Use the fact that tex2html_wrap_inline152

to write down a power series representation of the logarithmic function

. What is the center of the power series? For what values of x will this representation be valid? You might want to check your answer graphically, if you have a graphing calculator or access to a Math software program.

Click here to see the answers and to continue.

Helmut Knaust
Wed Jul 10 13:02:07 MDT 1996