 Techniques of Integration: Trigonometric substitutions
Techniques of Integration: Trigonometric substitutions  Techniques of Integration: Trigonometric substitutions
Techniques of Integration: Trigonometric substitutions

The familiar trigonometric identities
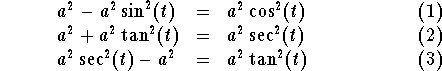
may be used to eliminate radicals from integrals. Specially when
these integrals involve ![]() and
and ![]() .
.
The expressions ![]() and
and
![]() should be seen as a constant plus-minus a square of a
function. In this case, x represents a function and a a constant.
For example
should be seen as a constant plus-minus a square of a
function. In this case, x represents a function and a a constant.
For example ![]() can be seen as one of the two previous
expressions. Indeed, if we
complete the square we get
can be seen as one of the two previous
expressions. Indeed, if we
complete the square we get
![]()
where ![]() . So from the above substitutions, we will set
. So from the above substitutions, we will set ![]() .
.
The following examples illustrate how to use trigonometric substitutions :

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Mohamed Amine Khamsi