 Integrating Powers and Product of Sines and Cosines
Integrating Powers and Product of Sines and Cosines  Integrating Powers and Product of Sines and Cosines
Integrating Powers and Product of Sines and Cosines

These are integrals of the following form:
![]()
We have two cases: both m and n are even or at least one of them is
odd.
Suppose n is odd. Hence n = 2k +
1. So ![]() hold. Therefore, we have
hold. Therefore, we have
![]()
which suggests the substitution ![]() . Indeed, we have
. Indeed, we have ![]() and hence
and hence
![]()
The latest integral is a polynomial function of u which is easy to
integrate.
Remark. Note that if m is odd, then we
will split ![]() and carry the same calculations. In this case,
the substitution will be
and carry the same calculations. In this case,
the substitution will be ![]() .
.
The main idea behind is to use the trigonometric identities
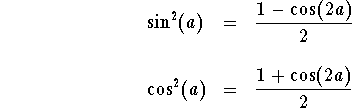
Remark. The following two formulas may be helpful in integrating powers of sine and cosine.
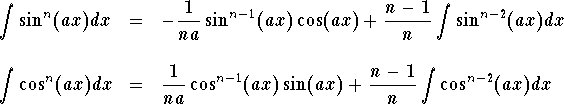

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Mohamed Amine Khamsi