Other Trigonometric Powers
Other Trigonometric Powers
These are integrals of the form
In every single one of these integrals, we will develop what is commonly called a Reduction Formula. The main idea behind is a smart use of trigonometric identities. Let us describe how it works.
, set
, set
, set
, set
Let us show how one can generate a reduction formula for .
The other once, will be given without any proof. We have
Since the derivative of 
is 
, we get
Therefore, we have
This is the reduction formula associated to the tangent function. What
it says is that in order to find the integral of it is
enough to find the integral of 
. This way, we can
reduce the power n all the way down to 1 or 0. Recall that
. Let us give a
table for all the reduction formulas.
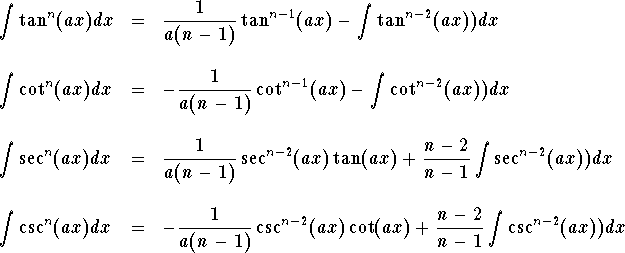
where a is an arbitrary constant and 
.
Remark. Note that for 
and
when n is even can be handled in a easier way.
Indeed, we have
which suggests the substitution 
. The same idea works
for the cosecant function (in this case, the substitution will be 
).
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author: Mohamed Amine Khamsi