 Integration by Parts: Example 4
Integration by Parts: Example 4 Integration by Parts: Example 4
Integration by Parts: Example 4
Evaluate
![]()
Looking at the two functions
involved in this example, we see that the function x is easy to
integrate or differentiate. The real problem is how to handle
![]() . First it is not clear how to integrate this one but
its derivative is the rational function
. First it is not clear how to integrate this one but
its derivative is the rational function 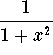 . Therefore this suggests the following
. Therefore this suggests the following
![]()
which implies
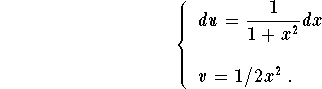
The integration by parts formula gives
![]()
The new integral will be handled by using the technique of integrating rational functions. But we can also do the following (which comes up doing the same ideas used in partial fraction decomposition)
![]()
Using this we get
![]()
The main idea behind this example is
valid for many other functions such as: ![]() ,
,
![]() , etc.. In fact, this is how the integration by parts
should be carried whenever the integral is given as a product of
f(x) and one the previous inverse-functions, try to integrate f(x)
and differentiate the inverse-function. The same remark holds for the
function
, etc.. In fact, this is how the integration by parts
should be carried whenever the integral is given as a product of
f(x) and one the previous inverse-functions, try to integrate f(x)
and differentiate the inverse-function. The same remark holds for the
function ![]() .
.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Mohamed Amine Khamsi