 Integration by Parts: Example 2
Integration by Parts: Example 2 Integration by Parts: Example 2
Integration by Parts: Example 2
Evaluate
![]()
First let us point out that we
have a definite integral. Therefore the final answer will be a number
not a function of x! Since the derivative or the integral of ![]() lead to the same function, it will not matter whether we do one
operation or the other. Therefore, we concentrate on the other
function
lead to the same function, it will not matter whether we do one
operation or the other. Therefore, we concentrate on the other
function ![]() . Clearly, if we integrate we will increase the power.
This suggests that we should differentiate
. Clearly, if we integrate we will increase the power.
This suggests that we should differentiate ![]() and integrate
and integrate ![]() .
Hence
.
Hence
![]()
After integration and differentiation, we get
![]()
The integration by parts formula gives
![]()
It is clear that the new integral 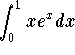 is not
easily obtainable. Due to its similarity with the initial integral,
we will use integration by parts for a second time. The same
discussion as before leads to
is not
easily obtainable. Due to its similarity with the initial integral,
we will use integration by parts for a second time. The same
discussion as before leads to
![]()
which implies
![]()
The integration by parts formula gives
![]()
Since 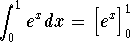 , we get
, we get
![]()
which finally implies
![]()
Easy calculations give
![]()
From this example, try to remember
that most of the time the integration by parts will not be enough to
give you the answer after one shot. You may need to do some extra
work: another integration by parts or use other techniques,....

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Mohamed Amine Khamsi