Problems on Improper IntegralsProblems on Improper Integrals
Exercise 1. Decide on the convergence or divergence of
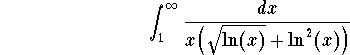
Answer. First notice that the denominator is equal to 0 when
x=1. Then the function inside the integral sign is unbounded at
x=1. Hence we have two bad points 1 and 
. So we must split
the integral and write
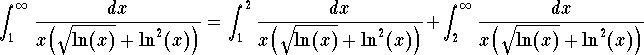
Let us first take care of the integral
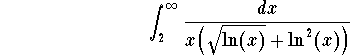
We have
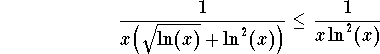
Since (by Bertrand's test) the improper integral
is convergent, then by the comparison test the improper integral
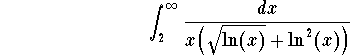
Next we take care of the integral
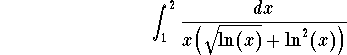
First notice that when 
, then
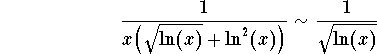
One may check this by showing that
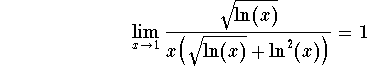
On the other hand (and this is the crucial step in this exercise) is
to find a polynomial approximation of 
when .
This will be done via Taylor polynomials. Indeed, we have
when , which gives
Hence we have
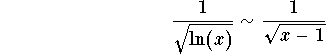
which implies
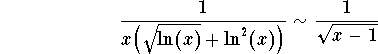
when . The p-test implies that the improper integral
is convergent. Therefore the limit test implies that the improper integral
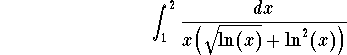
is convergent. Putting the two integrals together, we conclude that the improper integral
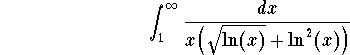
is convergent.
Exercise 2. Decide on the convergence or divergence of
Answer. The term 
is never equal for 
.
So let us focus on the term 
. According to the domain of the
tangent function, the only bad points we have to worry about is
. Clearly we have
Hence we have an improper integral or Type I at the bad point .
Clearly we have
when 
. So let us approximate 
when . Again we will use
Taylor polynomials, we have
when . This gives
when . Putting the stuff together we get
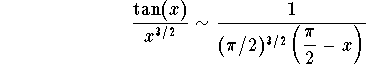
The p-test implies that the improper integral
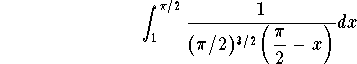
is divergent. Therefore the improper integral
is divergent.
Exercise 3. Decide on the convergence or divergence of
Answer. The only improper behavior is around . Hence
this integral is of Type II not of Type I. Therefore no need for
splitting it. Note that when 
, then 
. Hence
when . The p-test implies that the improper integral
is convergent. Therefore the limit test implies that the improper integral
is convergent.
Problem 1. First decide on the convergence and divergence of
Then evaluate f(x).
Problem 2. Assume that 
is
continuous. Find 
, where
Problem 3. Consider the function
Find f(x).
Problem 4. Evaluate
Problem 5. In this problem, we will evaluate
which 
function (that is f is differentiable and f' is continuous). Show
that
Problem 6. Decide on convergence or divergence of
where x > 0 and 
is any real number.
Problem 7. Decide on convergence or divergence of
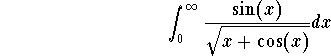
Problem 8. Decide on convergence or divergence of
If I is convergent, evaluate it.
Problem 9. Find
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi