 Improper Integrals: Introduction
Improper Integrals: Introduction Improper Integrals: Introduction
Improper Integrals: Introduction

Recall that the definition of an integral 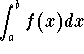 requires the function f(x) to be bounded on the bounded
interval [a,b] (where a and b are two real numbers). It is
natural then to wonder what happens to this definition if
requires the function f(x) to be bounded on the bounded
interval [a,b] (where a and b are two real numbers). It is
natural then to wonder what happens to this definition if
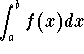 is improper.
is improper.
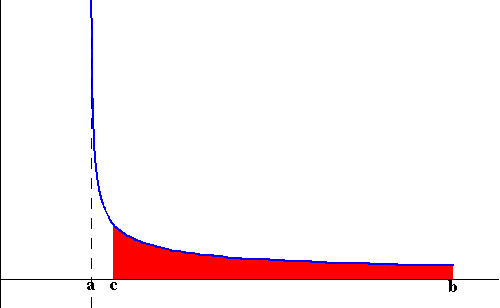
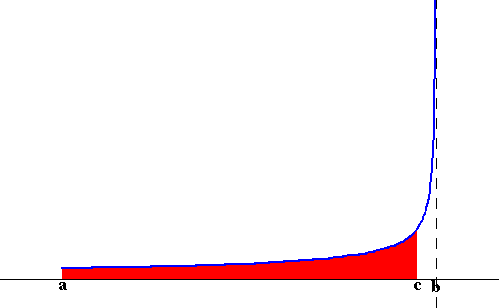
Case Type I: Consider the function f(x) defined on the interval [a,b] (where a and b are real numbers). We have two cases f(x) becomes unbounded around a or unbounded around b (see the images below)
|
and
|
For the sake of illustration, we considered a positive function. The
integral 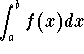 represents the area of the
region bounded by the graph of f(x), the x-axis and the lines x=a
and x=b. Assume f(x) is unbounded at a. Then the trick behind
evaluating the area is to compute the area of the region bounded by
the graph of f(x), the x-axis and the lines x=c and x=b. Then
we let c get closer and closer to a (check the figure below)
represents the area of the
region bounded by the graph of f(x), the x-axis and the lines x=a
and x=b. Assume f(x) is unbounded at a. Then the trick behind
evaluating the area is to compute the area of the region bounded by
the graph of f(x), the x-axis and the lines x=c and x=b. Then
we let c get closer and closer to a (check the figure below)
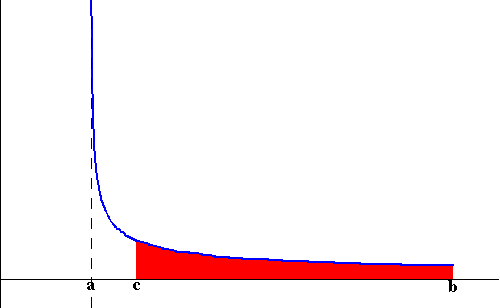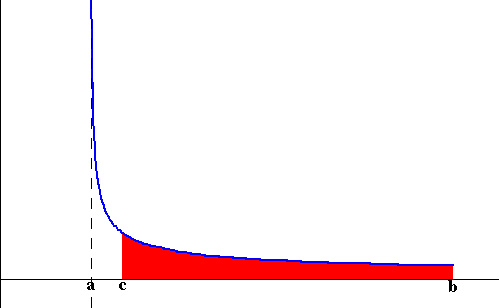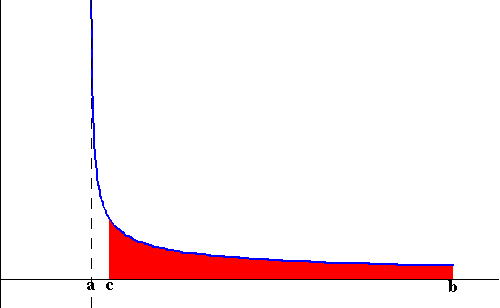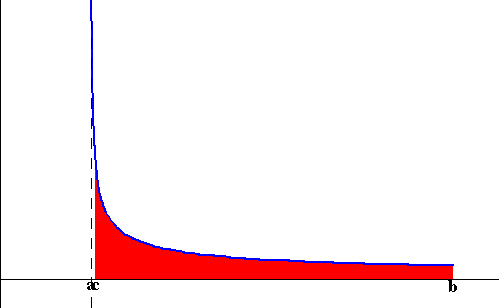
|
Hence we have
![]()
Note that the integral 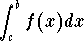 is well
defined. In other words, it is not an improper integral.
is well
defined. In other words, it is not an improper integral.
If the function is unbounded at b, then we will have
![]()
Remark. What happened if the function f(x) is unbounded at
more than one point on the interval [a,b]?? Very easy, first you
need to study f(x) on [a,b] and find out where the function is
unbounded. Let us say that f(x) is unbounded at ![]() and
and ![]() for
example, with
for
example, with ![]() . Then you must choose a
number
. Then you must choose a
number ![]() between
between ![]() and
and ![]() (that is
(that is ![]() )
and then write
)
and then write
![]()
Then you must evaluate every single integral to obtain the integral
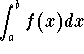 . Note that the single integrals do
not present a bad behavior other than at the end points (and not for
both of them).
. Note that the single integrals do
not present a bad behavior other than at the end points (and not for
both of them).
Example. Consider the function 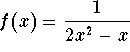 defined on [0,1]. It is easy to see that f(x)
is unbounded at x = 0 and
defined on [0,1]. It is easy to see that f(x)
is unbounded at x = 0 and ![]() .
Therefore, in order to study the integral
.
Therefore, in order to study the integral
![]()
we will write
![]()
and then study every single integral alone.
Case Type II: Consider the function f(x) defined
on the interval ![]() or
or ![]() . In other words, the
domain is unbounded not the function (see the figures below).
. In other words, the
domain is unbounded not the function (see the figures below).
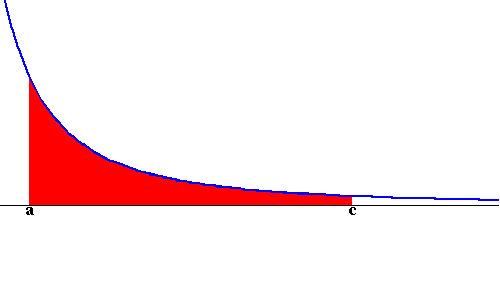
|
and
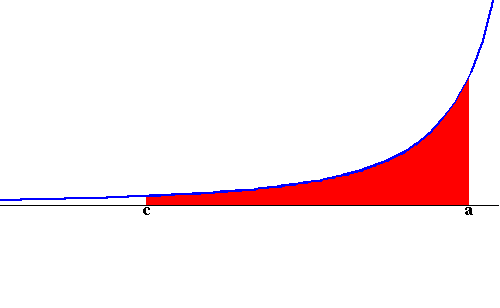
|
The same as for the Type I, we considered a positive function just for the sake of illustrating what we are doing. The following picture gives a clear idea about what we will do (using the area approach)
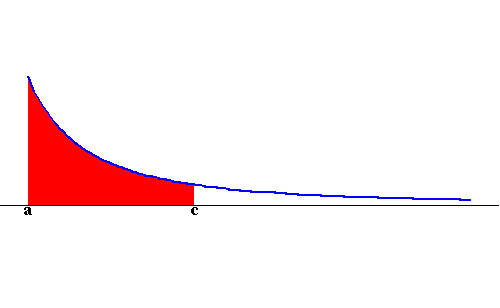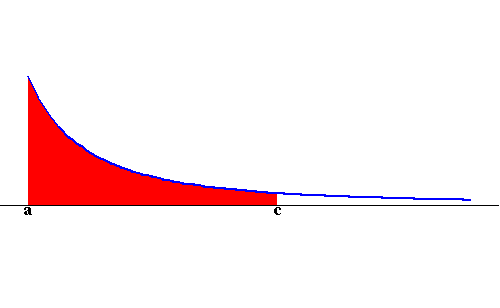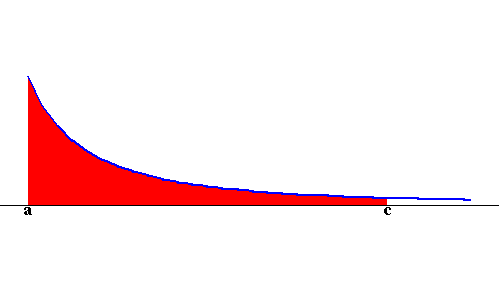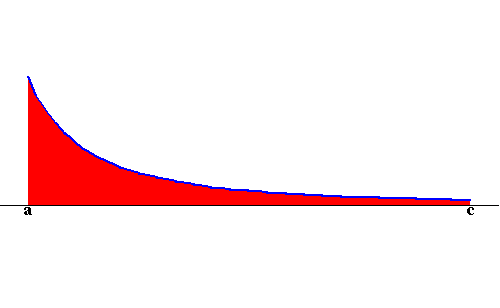
|
So we have
![]()
and
![]()
Example. Consider the function 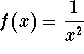 defined on
defined on ![]() . We have
. We have
![]()
On the other hand, we have
![]()
Hence we have
![]()
It may happen that the function f(x) may have Type I and Type II behaviors at the same time. For example, the integral
![]()
is one of them. As we did before, we must always split the integral into a sum of integrals with one improper behavior (whether Type I or Type II) at the end points. So for example, we have
![]()
The number 1 may be replaced by any number between 0 and ![]() since the function
since the function 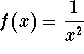 has a Type I
behavior at 0 only and of course a Type II behavior at
has a Type I
behavior at 0 only and of course a Type II behavior at ![]() .
.
Convergence and Divergence of improper integrals will be discussed in the next pages.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi