The Gamma Function

Many important functions in applied sciences are defined via improper integrals. Maybe the most famous among them is the Gamma Function. This is why we thought it would be a good idea to have a page on this function with its basic properties. You may consult any library for more information on this function.

Historically the search for a function generalizing the factorial expression for the natural numbers was on. In dealing with this problem one will come upon the well-known formula

A very quick approach to this problem suggests to replace n by x in the improper integral to generate the function

Clearly this definition requires a close look in order to determine the domain of f(x). The only possible bad points are 0 and . Let us look at the point 0. Since when , then we have

when . The p-test implies that we have convergence around 0 if and only if -x < 1 (or equivalently x >-1). On the other hand, it is quite easy to show that the improper integral is convergent at regardless of the value of x. So the domain of f(x) is . If we like to have as a domain, we will need to translate the x-axis to get the new function

which explains somehow the awkward term x-1 in the power of t. Now the domain of this new function (called the Gamma Function) is . The above formula is also known as Euler's second integral (if you wonder about Euler's first integral, it is coming a little later).

Basic Properties of

First, from the remarks above we have

One of the most important formulas satisfied by the Gamma function is

for any x > 0. In order to show this formula from the definition of , we will use the following identity

(this is just an integration by parts). If we let a goe to 0 and b goe to , we get the desired identity.

In particular, we get

for any x > 0 and any integer . This formula makes it possible for the function to be extended to (except for the negative integers). In particular, it is enough to know on the interval (0,1] to know the function for any x > 0. Note that since

we get . Combined with the above identity, we get what we expected before :

A careful analysis of the Gamma function (especially if we notice that is a convex function) yields the inequality

or equivalently

for every and x >0. If we let n goe to , we obtain the identity

Note that this formula identifies the Gamma function in a unique fashion.

Weierstrass identity. A simple algebraic manipulation gives

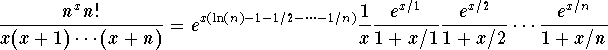
Knowing that the sequence converges to the constant -C, where

$$C = \lim_{n \rightarrow +\infty} 1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} - \ln(n)$$

is the Euler's constant. We get

$$\Gamma(x) = e^{-Cx} \frac{1}{x} \lim_{n \rightarrow +\infty} \prod_{k=1}^{k=n} \frac{e^{x/k}}{1 + x/k}$$

or

$$\Gamma(x) = e^{-Cx} \frac{1}{x} \prod_{n=1}^{+\infty} \frac{e^{x/n}}{1 + x/n} \cdot$$

The logarithmic derivative of the Gamma function: Since for any x >0, we can take the logarithm of the above expression to get

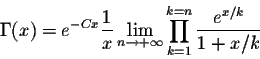
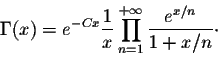
If we take the derivative we get

or

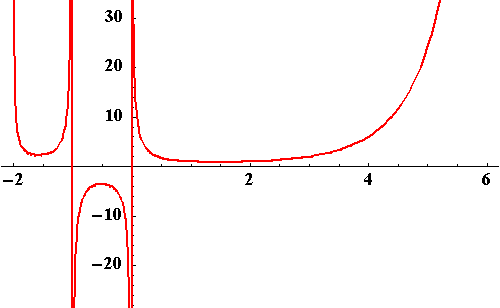
In fact, one can differentiate the Gamma function infinitely often. In "analysis" language we say that is of -class. Below you will find the graph of the Gamma function.

The Beta Function

Euler's first integral or the Beta function: In studying the Gamma function, Euler discovered another function, called the Beta function, which is closely related to . Indeed, consider the function

It is defined for two variables x and y. This is an improper integral of Type I, where the potential bad points are 0 and 1. First we split the integral and write

When , we have

and when , we have

So we have convergence if and only if x > 0 and y >0 (this is done via the p-test). Therefore the domain of B(x,y) is x > 0 and y>0. Note that we have

Let a and b such that , we have (via an integration by parts)

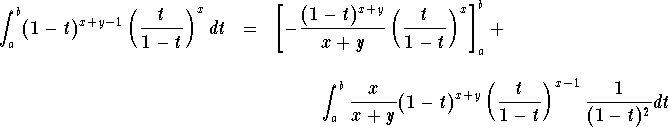
If we let a goe to 0 and b goe to 1, we will get

Using the properties of the Gamma function, we get

or

In particular, if we let x=y = 1/2, we get

If we set or equivalently , then the technique of substitution implies

Hence we have

or

Using this formula, we can now easily calculate the value of .

Other Important Formulas:

The following formulas are given without detailed proofs. We hope they will be of some interest.

Asymptotic behavior of the Gamma function when x is large: We have

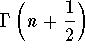where

If we take, x=n, we get after multiplying by n

This is a well known result, called Stirling's formula. So for large n, we have

The connection with : For any x > 0, we have

which implies

Using the Weierstrass product formula (for and ), we get

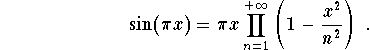
If we use the Beta function (B(x,y)), we get the following formulas:

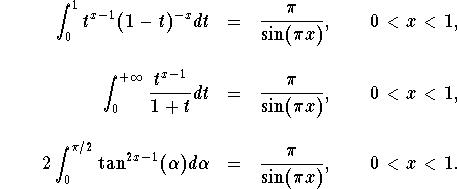
This page is inspired by Emil Artin's book on the Gamma Function. The exact reference is: Artin, Emil. The Gamma Function. New York, NY: Holt, Rinehart and Winston, 1964.

[Geometry] [Algebra] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra] [Trigonometry]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour