 Convergence and Divergence of Improper Integrals
Convergence and Divergence of Improper Integrals Convergence and Divergence of Improper Integrals
Convergence and Divergence of Improper Integrals

Consider a function f(x) which exhibits a Type I or Type II behavior
on the interval [a,b] (in other words, the integral 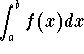 is improper). We saw before that the this integral
is defined as a limit. Therefore we have two cases:
is improper). We saw before that the this integral
is defined as a limit. Therefore we have two cases:
If the improper integral 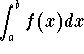 is split into
a sum of improper integrals (because f(x) presents more than one
improper behavior on [a,b]), then the integral converges if and only
if any single improper integral is convergent.
is split into
a sum of improper integrals (because f(x) presents more than one
improper behavior on [a,b]), then the integral converges if and only
if any single improper integral is convergent.
Example. Consider the function 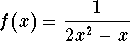 on [0,1]. We have
on [0,1]. We have
![]()
Therefore the improper integral
![]()
converges if and only if the improper integrals
![]()
are convergent. In other words, if one of these integrals is
divergent, the integral 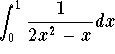 will be divergent.
will be divergent.
The p-integrals Consider the function 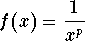 (where p > 0) for
(where p > 0) for ![]() . Looking at
this function closely we see that f(x) presents an improper behavior
at 0 and
. Looking at
this function closely we see that f(x) presents an improper behavior
at 0 and ![]() only. In order to discuss convergence or
divergence of
only. In order to discuss convergence or
divergence of
![]()
we need to study the two improper integrals
![]()
We have
![]()
and
![]()
For both limits, we need to evaluate the indefinite integral
![]()
We have two cases:
![]()
![]()
In order to decide on convergence or divergence of the above two improper integrals, we need to consider the cases: p<1, p=1 and p >1.
![]()
and
![]()
![]()
and
![]()
![]()
and
![]()
The p-Test: Regardless of the value of the number p, the improper integral
![]()
is always divergent. Moreover, we have
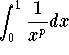 is
convergent if and only if p <1
is
convergent if and only if p <1
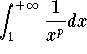 is
convergent if and only if p >1
is
convergent if and only if p >1
In the next pages, we will see how some easy tests will help in deciding whether an improper integral is convergent or divergent.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi