 More Problems on the Derivative
More Problems on the Derivative  More Problems on the Derivative
More Problems on the Derivative In these pages we discuss some problems related to the derivative concept. Most of the problems are challenging and not easy. We will give the answer to some of them The readers are encouraged to find the solutions for the rest. Send it and we will publish it. Enjoy.
Problem 1. Show that the function
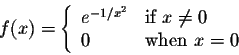
Problem 2. Let f(x) be a function defined on (-a,a), with a > 0. Assume that f(x) is continuous at 0 and
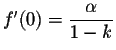 .
.
Answer.
Problem 4. Let f(x) be a differentiable function. Assume that f'(x) is continuous. Define the sequence ![]() by
by
Problem 5. Consider the function
f(x) = (x2-1)n, for ![]() .
Show that
.
Show that
Answer.
Problem 6. Consider the function
![]() .
Show that
.
Show that
Problem 7. Let
![]() ,
where
,
where
![]() .
Let a and b be such that
.
Let a and b be such that
Problem 8. Show that ex = 1-x has a unique solution. Then find that solution.
Answer.
Problem 9. Show that for any
![]() ,
we have
,
we have
Answer.
Problem 10. Show that for any a and b such that 0 < a< b, we have
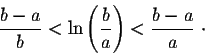
Answer.
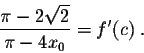
 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi