Critical Points

We will discuss the occurrence of local maxima and local minima of a function. In fact, these points are crucial to many questions related to optimization problems. We will discuss these problems in later pages.

Definition. A function f(x) is said to have a local maximum at c iff there exists an interval I around c such that

$$f(c) \geq f(x) \;\;\mbox{for all $x \in I$}.$$

Analogously, f(x) is said to have a local minimum at c iff there exists an interval I around c such that

$$f(c) \leq f(x) \;\;\mbox{for all $x \in I$}.$$

A local extremum is a local maximum or a local minimum.

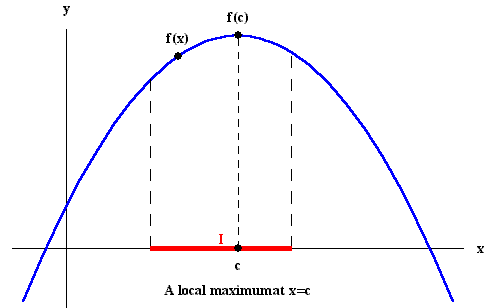Using the definition of the derivative, we can easily show that:

If f(x) has a local extremum at c, then either

$$f'(c) = 0\;\;\mbox{or $f'(c)$ does not exist.}$$

These points are called critical points.

Example. Consider the function f(x) = x³. Then f'(0) = 0 but 0 is not a local extremum. Indeed, if x < 0, then f(x) < f(0) and if x > 0, then f(x) > f(0).

Therefore the conditions

$$f'(c) = 0\;\;\mbox{or $f'(x)$ does not exist.}$$

do not imply in general that c is a local extremum. So a local extremum must occur at a critical point, but the converse may not be true.

Example. Let us find the critical points of

f(x) = |x²-x|

Answer. We have

$$f(x) = \left\{\begin{array}{clcll} x^2-x &\mbox{if}& \;\; x \... ...leq 1\\ x^2-x &\mbox{if}& \;\; 1 \leq x.\\ \end{array}\right.$$

Clearly we have

$$f'(x) = \left\{\begin{array}{clcll} 2x-1 &\mbox{if}& \;\; x <... ... 0< x < 1\\ 2x-1 &\mbox{if}& \;\; 1 < x.\\ \end{array}\right.$$

Clearly we have

$$f'(x) = 0 \;\;\mbox{iff}\;\; x = \frac{1}{2}\cdot$$

Also one may easily show that f'(0) and f'(1) do not exist. Therefore the critical points are

$$\frac{1}{2},\;0,\;1.$$

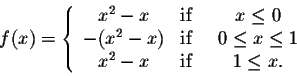
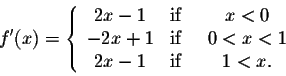
Let c be a critical point for f(x). Assume that there exists an interval I around c, that is c is an interior point of I, such that f(x) is increasing to the left of c and decreasing to the right, then c is a local maximum. This implies that if $f'(x) \geq 0$ for $x \leq c$ (x close to c), and $f'(x) \leq 0$ for $x \geq c$ (x close to c), then c is a local maximum. Note that similarly if $f'(x) \leq 0$ for $x \leq c$ (x close to c), and $f'(x) \geq 0$ for $x \geq c$(x close to c), then c is a local minimum.

So we have the following result:

First Derivative Test. If c is a critical point for f(x), such that f '(x) changes its sign as x crosses from the left to the right of c, then c is a local extremum.

Example. Find the local extrema of

f(x) = |x²-x|

Answer. Since the local extrema are critical points, then from the above discussion, the local extrema, if they exist, are among the points

$$\frac{1}{2},\;0,\;1.$$

Recall that

$$f'(x) = \left\{\begin{array}{clcll} 2x-1 &\mbox{if}& \;\; x <... ... 0< x < 1\\ 2x-1 &\mbox{if}& \;\; 1 < x.\\ \end{array}\right.$$

(1)

For x = 1/2, we have

$$\left\{\begin{array}{clcll} f'(x) > 0 &\mbox{if}& \;\; 0 < x ... ... f'(x) < 0 &\mbox{if}& \;\; 1/2 < x < 1.\\ \end{array}\right.$$

So the critical point $\frac{1}{2}$ is a local maximum.

(2)

For x = 0, we have

$$\left\{\begin{array}{clcll} f'(x) < 0 &\mbox{if}& \;\; x <0\\ f'(x) > 0 &\mbox{if}& \;\; 0< x < 1/2.\\ \end{array}\right.$$

So the critical point 0 is a local minimum.

(3)

For x = 1, we have

$$\left\{\begin{array}{clcll} f'(x) < 0 &\mbox{if}& \;\; 1/2 < x <1\\ f'(x) > 0 &\mbox{if}& \;\; 1 < x .\\ \end{array}\right.$$

So the critical point -1 is a local minimum.

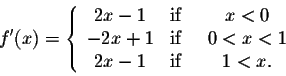
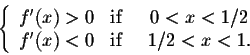
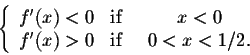
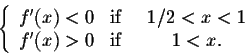
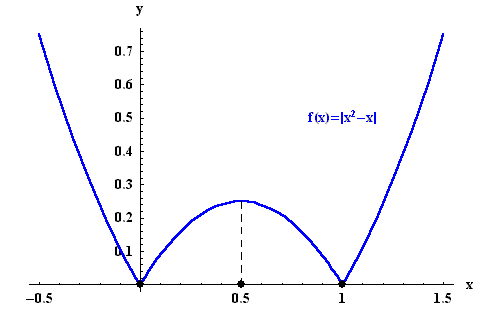Let c be a critical point for f(x) such that f'(c) =0.

(i)

If f''(c) > 0, then f'(x) is increasing in an interval around c. Since f'(c) =0, then f'(x) must be negative to the left of c and positive to the right of c. Therefore, c is a local minimum.

(ii)

If f''(c) < 0, then f'(x) is decreasing in an interval around c. Since f'(c) =0, then f'(x) must be positive to the left of c and negative to the right of c. Therefore, c is a local maximum.

This test is known as the Second-Derivative Test.

Example. Find the local extrema of

f(x) = x⁵ - 5 x.

Answer. First let us find the critical points. Since f(x) is a polynomial function, then f(x) is continuous and differentiable everywhere. So the critical points are the roots of the equation f'(x) = 0, that is 5x⁴ - 5 = 0, or equivalently x⁴ - 1 =0. Since x⁴ - 1 = (x-1)(x+1)(x²+1), then the critical points are 1 and -1. Since f''(x) = 20 x³, then

$$f''(1) = 20 > 0 \;\;\mbox{and}\;\; f''(-1) = -20 < 0.$$

The second-derivative test implies that x=1 is a local minimum and x= -1 is a local maximum.

Exercise 1. Find the local extrema of

$$f(x) = \frac{x}{1+x^2}\cdot$$

Answer.

Exercise 2. Find the local extrema of

$$f(x) = \sin(x) + \cos(x).$$

Answer.

[Back] [Next] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2023 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour