The Derivatives of Trigonometric Functions - Exercise 2

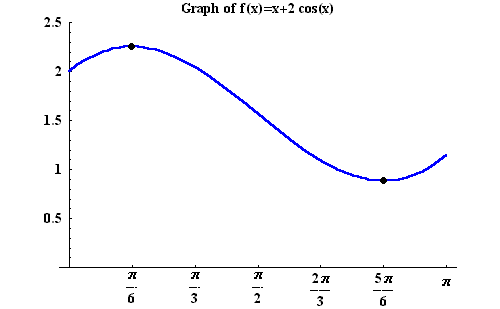
Exercise 2. Find the x-coordinates of all points on the graph of $f(x) = x +2\cos(x)$ in the interval $[0,\pi]$ at which the tangent line is horizontal.

Answer. The points (x,f(x)) at which the tangent line is horizontal are the ones for which f'(x) = 0. Let us first find f'(x). We have

$$f'(x) = 1 - 2\sin(x)\;.$$

So we have to solve $1 - 2\sin(x) = 0$ which gives $\sin(x) = 1/2$. We get

$$x = \frac{\pi}{6}\;\;\mbox{or}\;\; x = \pi - \frac{\pi}{6} = \frac{5\pi}{6} \cdot$$

[Back] [Next] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour