The Derivatives of Trigonometric Functions - Exercise 1

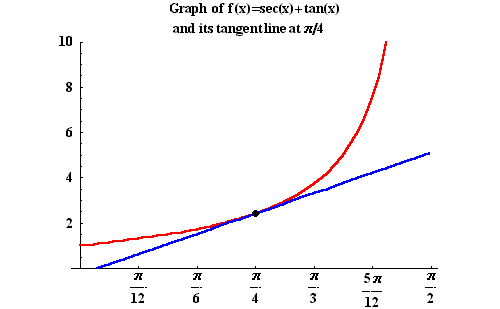
Exercise 1. Find the equations of the tangent line and the normal line to the graph of $f(x) = \sec(x) + \tan(x)$ at the point $\left(\displaystyle \frac{\pi}{4}, f\left(\frac{\pi}{4}\right)\right)$.

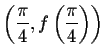Answer. First we need to find the derivative of f(x) so we can get the slope of the tangent line and the normal line. We have

$$f'(x) = \sec(x) \tan(x) + \sec^2(x)\;.$$

So we have

$$f'\left(\frac{\pi}{4}\right) = \sqrt{2} + 2$$

knowing that $\sec(\pi/4) = \sqrt{2}$ and $\tan(\pi/4) = 1$. Note that

$$f\left(\frac{\pi}{4}\right) = \sqrt{2} + 1\;.$$

So the equation of the tangent line at the point $(\pi/4, \sqrt{2} + 1)$ is

$$y - \sqrt{2} - 1 = (\sqrt{2} + 2) \left(x- \frac{\pi}{4}\right) \;.$$

the slope of the normal line to the graph at the point $(\pi/4, \sqrt{2} + 1)$ is

$$- \frac{1}{\sqrt{2} + 2}$$

which helps us find the equation of the normal line as

$$y - \sqrt{2} - 1 = - \frac{1}{\sqrt{2} + 2} \left(x- \frac{\pi}{4}\right) \;.$$

[Back] [Next] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour