 APPLICATIONS OF EXPONENTIAL AND
APPLICATIONS OF EXPONENTIAL AND  APPLICATIONS OF EXPONENTIAL AND
APPLICATIONS OF EXPONENTIAL AND 
(Interest Rate Word Problems)
1. To solve an exponential or logarithmic word problems, convert the narrative to an equation and solve the equation.

Problem 1: If you invested $1,000 in an account paying an annual
percentage rate (quoted rate) of 12%, compound quarterly, how
much would you have in you account at the end of 1 year, 10 years,
20 years, 100 years.
Answer: 1 year = $1,125.51,10 Years = $3,262.04, 20 years
= $10,640.89, 100 years = $136,423,718.23
Solution and Explanations:
![]()
where A is the balance at the end of a certain time period, P is the beginning investment, t is the number of years. The annual rate of 12% is converted to a quarterly interest rate since the compounding is quarterly (4 times per year). Take the annual interest rate of 12% and divide by 4 to obtain the quarterly interest rate. The exponent is 4t because there are 4 compounding periods in every year. Therefore, 4t represents the number of compounding periods during t years.
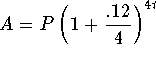 to derive A:
to derive A:
![]()
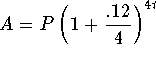 to derive A:
to derive A:
![]()
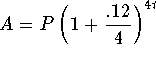 to derive A:
to derive A:
![]()
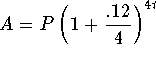 to derive A:
to derive A:
![]()
If you would like to work another problem and check the answer and solution, click on Problem.

 S.O.S MATHematics home page
S.O.S MATHematics home pageDo you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus