 APPLICATIONS OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS
APPLICATIONS OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS

(Interest Rate Word Problems)
1. To solve an exponential or logarithmic word problems, convert the narrative to an equation and solve the equation.

Example 2: A $5,000 investment is made in a trust fund at an
annual percentage rate of 10%, compounded annually. Predict
the balance in the account after 5 years. How long will it take
the investment to reach $15,500? Suppose that another bank
promised you that your account would reach $15,500 in 10 years,
what annual interest would the second bank be paying?
Explanation and Solution:
-
- Balance at the end of the first year: The trust account began
the year with the $5,000 investment and will have a balance
equal to the $5,000 plus the 10% interest on the $5,000 at
the end of the first year.
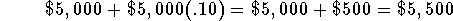
or 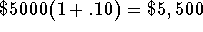 .
.
-
- Balance at the end of the second year: The trust account began the year with a balance of $5,500 investment and will have
a balance equal to the $5,500 plus the 10% interest on the
$5,500 at the end of the second year.
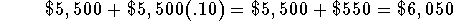
or 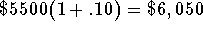 .
.
-
- Note that in terms of the initial investment, the above steps
could be written
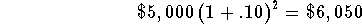
-
- Balance at the end of the third year: The trust account began the year with a balance of $6,050 investment and will have
a balance equal to the $6,050 plus the 10% interest on the
$6,050 at the end of the third year
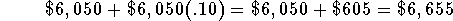
or 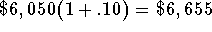 .
.
-
- Note that in terms of the initial investment, the above steps
could be written
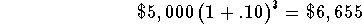
-
- Balance at the end of the fourth year: The trust account began the year with a balance of $6,655 investment will have a balance
equal to the $6,655 plus the 10% interest on the $6,655 at
the end of the second year
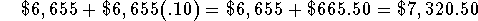
or 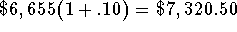
-
- Note that in terms of the initial investment, the above steps
could be written
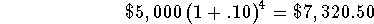
-
- Balance at the end of the fifth year: The trust account began
the year with a balance of $7,320.50 investment will have a
balance equal to the $7,320.50 plus the 10% interest on the
$7,320.50 at the end of the fifth year
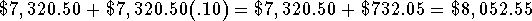
or 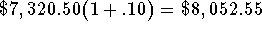
-
- Note that in terms of the initial investment, the above steps
could be written
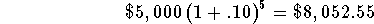
-
- If you deposit $5,000 in an account that pays 10% per year
with annually compounding, and you left the money in the account
for 5 years, you would have a balance of $8,052.55 at the end
of the 5 years.
-
- The second part of the problem was to estimate how many years it would take for the account to teach $15,500.
-
- In this problem, you know the starting amount, the ending amount, and the interest rate, what you are trying to determine is the
time
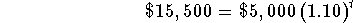
-
- Divide both sides by $5,000:

-
- Take the Log of both sides:
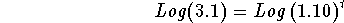
-
- Simplify the right side of the above equation using the third
rule of logarithms:
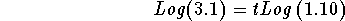
-
- Divide both sides of the above equation by Log(1.10):
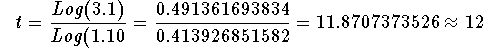
-
- This means that it takes almost 12 years for your account to
reach $15,500.
-
- The third part of the problem was to estimate the interest rate
if your $5,000 reached $15,500 in 10 years.
-
- In this problem, you know the starting amount, the ending amount, and the time, what you are trying to determine is the annual
interest rate
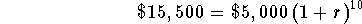
-
- Divide both sides of the above equation by $5,000:

-
- Take the Log of both sides of the above equation:
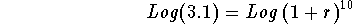
-
- Simplify the right side of the above equation using the third
rule of logarithms:
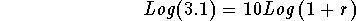
-
- Divide both sides of the above equation by 10:
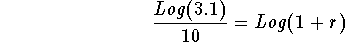
-
- Calculate the left side of the above equation:
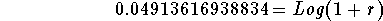
-
- Rewrite the logarithmic equation as an exponential equation with
base 10 and exponent 0.04913616938834:
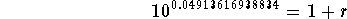
-
- Subtract 1 from both sides of the above equation:
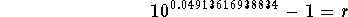
-
- Simplify the left side of the above equation:
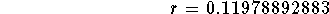
rounded to 0.1198
-
- This means that for the $1,000 to reach $15,500 in 10 years,
the bank would have to pay 11.98% interest, compounded annually.
If you would like to work another example, click on
Example.

[Next Example]
[Menu Back to Applications]
[Algebra]
[Trigonometry]
[Complex
Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: Nancy
Marcus
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 APPLICATIONS OF EXPONENTIAL AND
APPLICATIONS OF EXPONENTIAL AND  APPLICATIONS OF EXPONENTIAL AND
APPLICATIONS OF EXPONENTIAL AND 

![]()
![]() .
.
![]()
![]() .
.
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page