 PROPERTIES OF LOGARITHMS
PROPERTIES OF LOGARITHMS PROPERTIES OF LOGARITHMS
PROPERTIES OF LOGARITHMS
1. To solve a logarithmic equation, rewrite the equation in exponential form and solve for the variable.
Problem 2: Solve for x in the equation
![]()
Answer: 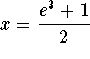 is the exact answer and
x=10.5427684616 is an approximate answer.
is the exact answer and
x=10.5427684616 is an approximate answer.
Solution:
![]()
![]()
![]()
![]()
is the exact answer and ![]() is an approximate answer.
is an approximate answer.
Check: Let's substitute the approximate value of the answer in the original equation and determine whether the left side of the equation equals the right side of the equation after the substitution. Remember we rounded the answer; therefore, the left and right sides of the equation will most likely be very close but may not equal
![]()
Since the value of the left side of the equation is 3 when you substitute x
= 10.5427684616, and the right side of the equal is 3, you have proved your answer.
If you would like to work on another problem, click on Problem.

 S.O.S MATHematics home page
S.O.S MATHematics home pageDo you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
