 SOLVING EXPONENTIAL EQUATIONS Problem 5
SOLVING EXPONENTIAL EQUATIONS Problem 5

To solve an exponential equation, take the log of both sides, and
solve for the variable.

Problem 5: Solve for x in the equation
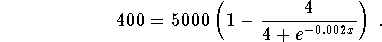
Solution:
-
- Step 1: Isolate the exponential term
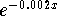 using steps 2 through 6.
using steps 2 through 6.
-
- Step 2: Divide both sides of the original equation by 5000:
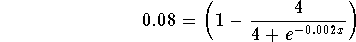
-
- Step 3: Subtract 1 from both sides of the above equation:
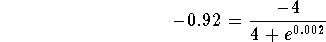
or

-
- Step 4: Multiply both sides of the above equation by
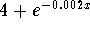 :
:
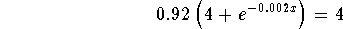
-
- Step 5: :Divide both sides of the above equation by 0.92:
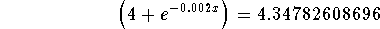
-
- Step 6: Subtract 4 from both sides of the above equation:
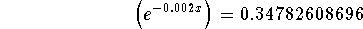
-
- Step 7: Take the natural log of both sides of the above equation:
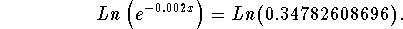
-
- Step 8: Simplify the left side of the above equation using Logarithmic Rule 3:
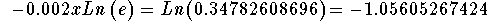
-
- Step 9: Since Ln(e) = 1, the above equation is simplified to
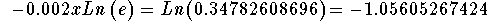
-
- Step 10: Divide both sides of the above equation by -0.002:
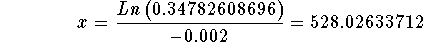
rounded to 528.
Check: Check the graph, it should cross in one place very close to x = 528. You can also substitute the number in the original equation and check to see if the left side of the equation then equals the right side of the equation.
If you want to work another problem, click on
Next Problem.

[Previous Problem]
[Next Problem]
[Menu Back to Solving EE]
[Algebra]
[Trigonometry]
[Complex
Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: Nancy
Marcus
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 SOLVING EXPONENTIAL EQUATIONS Problem 5
SOLVING EXPONENTIAL EQUATIONS Problem 5  SOLVING EXPONENTIAL EQUATIONS Problem 5
SOLVING EXPONENTIAL EQUATIONS Problem 5 

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page