 RULES OF LOGARITHMS - Problem 7
RULES OF LOGARITHMS - Problem 7

Let a be a positive number such that a does not equal 1, let
n be a real number, and let u and v be positive real numbers.
Logarithmic Rule 3: 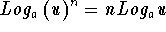 .
.

Problem 7: Simplify the following term completely
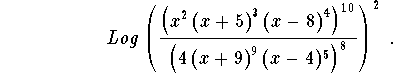
State the domain that makes your final answer equal to the original expression.
There are many ways to work the above problem; we have included one of the ways.
Solution:
-
- Step 1: The expression is of the form
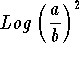 which can be simplified to the form
which can be simplified to the form 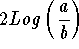 or
or
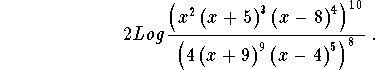
-
- Step 2: The expression
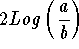 can be simplified to the form
can be simplified to the form 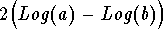 or
or 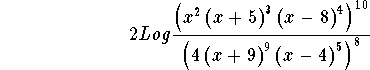
which can be written as
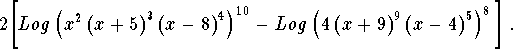
-
- Step 3: This last expression is of the form
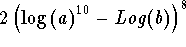 which can be simplified to
which can be simplified to
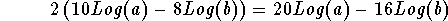
or in term of our problem
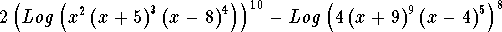
can be written as
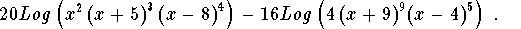
-
- Step 4: Both of these last terms are in the form
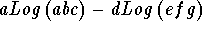 which can be simplified to the form
which can be simplified to the form
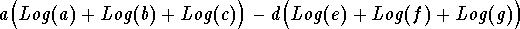
or in terms of our problem
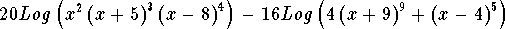
can be written as
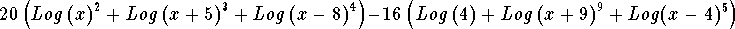
-
- Step 5: These terms can be simplified to
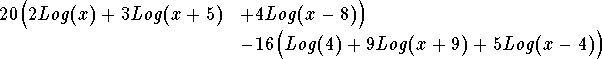
and again to
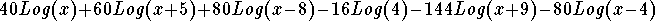
-
- Step 6: The first term will work if x > 0, the second term will work if x > -5, the third term will work if x > 8, the fourth term will always work, the fifth term will work if x > -9, and the last term will work if x > 4. If we choose the domain as x > 8, then the original expression
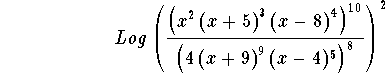
is equal to the final expression
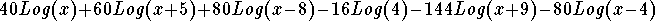
-
- Step 7: You can check answer by graphing both expression over the domain x >8. If you see just one graph, you have worked the problem correctly.
-
- Step 8: You can also check the answer by assigning x a value greater than 8 and substituting that value in both expressions. If the answers come out the same, you are correct. Let's let x = 10 in the original equation. If x = 10, the original equation has a value equal to
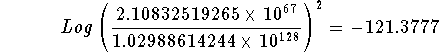
Let's let x = 10 in the final equation. If x = 10, the final equation has a
value equal to
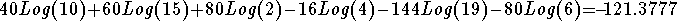
-
- Step 9: Pat yourself on the back because you have correctly worked the problem.
If you want to review the menu again, click on menu below.

[Previous Problem]
[Menu Back to Rule 3]
[Algebra]
[Trigonometry]
[Complex
Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: Nancy
Marcus
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 RULES OF LOGARITHMS - Problem 7
RULES OF LOGARITHMS - Problem 7  RULES OF LOGARITHMS - Problem 7
RULES OF LOGARITHMS - Problem 7 
![]() .
.
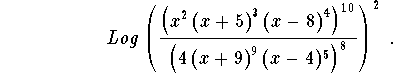
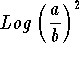 which can be simplified to the form
which can be simplified to the form 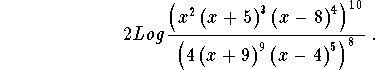
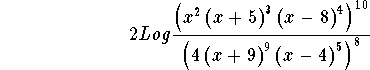
![]()
![]()
![]()
![]()
![]()
![]()
![]()
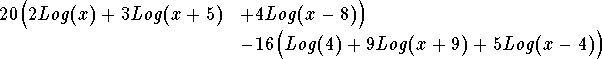
![]()
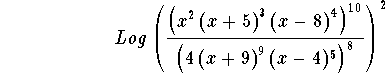
![]()
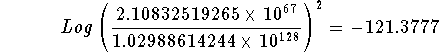
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page