 RULES OF LOGARITHMS - Problem 5
RULES OF LOGARITHMS - Problem 5

Let a be a positive number such that a does not equal 1, let
n be a real number, and let u and v be positive real numbers.
Logarithmic Rule 3: 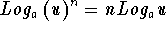 .
.

Problem 5: Simplify 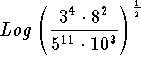 and calculate the value.
and calculate the value.
Answer: - 3.487
Solution : There are many ways to work the above problem. We have included two of the ways.
Solution 1:
-
- Step 1: First note that you are taking the log of an expression raised to a power; therefore, you use Rule 3.
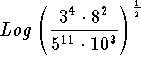 can be written
can be written 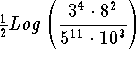 .
.
-
- Step 2: You will now be taking the log of a quotient; therefore, use Rule 2.
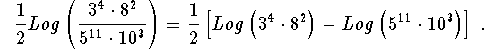
-
- Step 3: You will now be taking logs of products; therefore, use Rule 1.
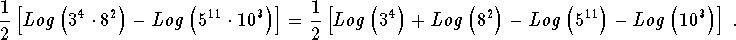
-
- Step 4: You will now be taking logs of expressions raised to a power, use Rule 3.
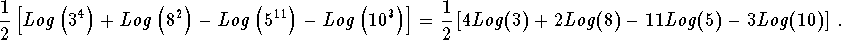
-
- Step 5: This last expression can be written
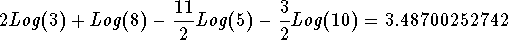
rounded to 3.487.
-
- Step 6: You can check your answer by calculating directly from the initial expression.
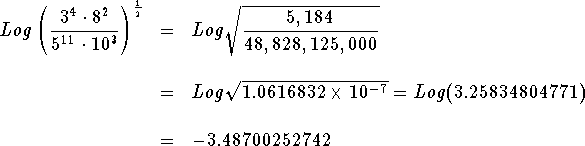
Since both answers are the same, you have correctly worked the problem.
Solution 2:
-
- Step 1: First note that you are taking the log of an expression raised to a power; therefore, you use Rule 3.
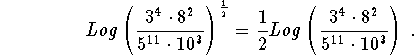
-
- Step 2: Simplify the numerator and simplify the denominator:
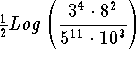 can be written
can be written
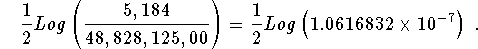
-
- Step 3: Calculate the logarithm:
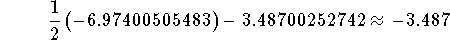
If you want to work another problem, click on Next Problem.

[Previous Problem]
[Next Problem]
[Menu Back to Rule 3]
[Algebra]
[Trigonometry]
[Complex
Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: Nancy
Marcus
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 RULES OF LOGARITHMS - Problem 5
RULES OF LOGARITHMS - Problem 5  RULES OF LOGARITHMS - Problem 5
RULES OF LOGARITHMS - Problem 5 
![]() .
.
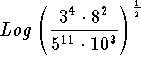 and calculate the value.
and calculate the value.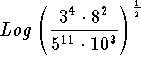 can be written
can be written 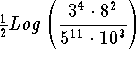 .
.![]()
![]()
![]()
![]()
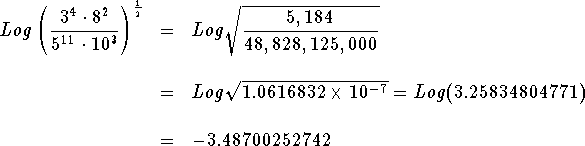
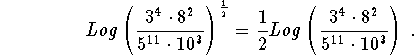
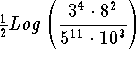 can be written
can be written
![]()
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page