 RULES OF LOGARITHMS - RULE 3
RULES OF LOGARITHMS - RULE 3
 RULES OF LOGARITHMS - RULE 3
RULES OF LOGARITHMS - RULE 3 
Let a be a positive number such that a does not equal 1, let
n be a real number, and let u and v be positive real numbers.
Logarithmic Rule 3: ![]() .
.

Example 1: Find ![]() two ways.
two ways.
Solution: Since ![]() can be written
can be written ![]() , the
expression
, the
expression ![]() can be written
can be written
![]()
which in turn can be written
![]()
We have
![]()
and
![]()
Example 2: Find ![]() .
.
Solution: The expression ![]() can be
written
can be
written ![]() which in turn can be written
which in turn can be written ![]() . This last expression can be
rewritten using Rule 1 as
. This last expression can be
rewritten using Rule 1 as
![]()
This represents 6 identical terms and we can
write the sum of the six terms as ![]() .
.
Check: The original expression ![]() can be written
can be written
![]()
The last expression ![]() can be written
can be written
![]()
If you would like to review another example, click on Example.
Work the following problems and if you want to check your answer, click on answer.
Problem 1: Find ![]()
Problem 2: Find ![]()
Problem 3: Simplify 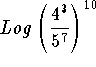
Problem 4: Simplify 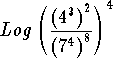
Problem 5: Simplify 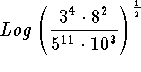
Problem 6: Simplify ![]() . What assumptions must you make before you can begin work on this problem?
. What assumptions must you make before you can begin work on this problem?
Problem 7: Simplify the following term completely
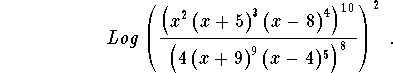
State the domain that makes your final answer equal to the original expression.

 S.O.S MATHematics home page
S.O.S MATHematics home pageDo you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus