RULES OF LOGARITHMS

Let a be a positive number such that a does not equal 1, let n be a real number, and let u and v be positive real numbers.

Logarithmic Rule 1:

Logarithmic Rule 2:

Logarithmic Rule 3:

Since logarithms are nothing more than exponents, these rules come from the rules of exponents. Let a be greater than 0 and not equal to 1, and let n and m be real numbers.

Exponential Rule 1:

Example: Let a = 5, n = 2, and m = 6. and

Exponential Rule 2: 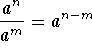tex2html_wrap_inline106

Example: Let a = 5, n = 2, and m = 6. 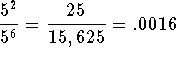tex2html_wrap_inline108 and

Exponential Rule 3:

Example: Let a = 5, n = 2, and m = 6. and

If you want to review exponential rules in detail with examples and problems, click on Exponential Rules.

If you want to review logarithmic rules in detail with examples and problems, click on one of the following rules.

Rule 1:

Rule 2:

Rule 3:

[Menu Back to Exponential Functions]

[Algebra] [Trigonometry] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus